R-squared (R2)
Es misst den Anteil der Variation in Ihrer abhängigen Variablen, der durch alle Ihre unabhängigen Variablen im Modell erklärt wird. Es wird davon ausgegangen, dass jede unabhängige Variable im Modell dazu beiträgt, Variationen in der abhängigen Variablen zu erklären., In Wirklichkeit helfen einige unabhängige Variablen (Prädiktoren) nicht, abhängige (Ziel -) Variablen zu erklären. Mit anderen Worten, einige Variablen tragen nicht zur Vorhersage der Zielvariablen bei.
Mathematisch wird das R-Quadrat berechnet, indem die Summe der Quadrate der Residuen (SSres) durch die Gesamtsumme der Quadrate (SStot) dividiert und dann von 1 subtrahiert wird. In diesem Fall misst SStot die Gesamtvariation. SSreg-Maßnahmen erläuterten Variation und SSres misst unerklärliche Variation.,
Als SSres + SSreg = SStot, R2 = Erklärte variation / Total Variation
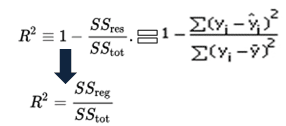
R-squared Gleichung
R-Squared wird auch als Bestimmtheitsmaß. Er liegt zwischen 0% und 100%. Ein r-Quadratwert von 100% bedeutet, dass das Modell alle Variationen der Zielvariablen erklärt. Und ein Wert von 0% misst die Null-Vorhersagekraft des Modells. Höherer R-Quadrat-Wert, besser das Modell.
Bereinigtes R-Quadrat
Es misst den Anteil der Variation, der nur durch die unabhängigen Variablen erklärt wird, die wirklich bei der Erklärung der abhängigen Variablen helfen., Es bestraft Sie für das Hinzufügen unabhängiger Variablen, die bei der Vorhersage der abhängigen Variablen nicht helfen.
Angepasst R-Quadrat kann mathematisch in Bezug auf die Summe der Quadrate berechnet werden. Der einzige Unterschied zwischen der R-Quadrat-und der angepassten R-Quadrat-Gleichung ist der Freiheitsgrad.
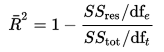
Angepasste R-Quadratgleichung
In der obigen Gleichung ist dft der Freiheitsgrad n– 1 der Schätzung der Populationsvarianz der abhängigen Variablen und dfe der Freiheitsgrad n – p – 1 der Schätzung der zugrunde liegenden Populationsfehlervarianz.,
Angepasst R-Quadrat-Wert kann basierend auf Wert von r-Quadrat, Anzahl der unabhängigen Variablen (Prädiktoren), Gesamtstichprobengröße berechnet werden.

Angepasste R-Quadratgleichung 2
Differenz zwischen R-Quadrat und angepasstem R-Quadrat
- Jedes Mal, wenn Sie einem Modell eine unabhängige Variable hinzufügen, erhöht sich das R-Quadrat, auch wenn die unabhängige Variable unbedeutend ist. Es nimmt nie ab. Während das angepasste R-Quadrat nur dann zunimmt, wenn die unabhängige Variable signifikant ist und die abhängige Variable beeinflusst.,
- Adjusted r-squared kann negativ sein, wenn r-squared ist nahe null.
- Der angepasste R-Quadrat-Wert muss immer kleiner oder gleich dem R-Quadrat-Wert sein.
In der folgenden Tabelle ist das angepasste r-Quadrat maximal, wenn wir zwei Variablen enthalten. Es nimmt ab, wenn die dritte Variable hinzugefügt wird. Während r-squared zunimmt, wenn wir die dritte Variable einbeziehen. Dies bedeutet, dass die dritte Variable für das Modell unbedeutend ist.

R-Squared vs. Adjusted R-Squared
Das R-Quadrat sollte verwendet werden, um Modelle mit einer unterschiedlichen Anzahl unabhängiger Variablen zu vergleichen. Das angepasste R-Quadrat sollte bei der Auswahl wichtiger Prädiktoren (unabhängige Variablen) für das Regressionsmodell verwendet werden.
R : Berechnen Sie das R-Quadrat und das angepasste R-Quadrat
Angenommen, Sie haben tatsächliche und vorhergesagte abhängige Variablenwerte. Im folgenden Skript haben wir ein Beispiel dieser Werte erstellt. In diesem Beispiel bezieht sich y auf die beobachtete abhängige Variable und yhat auf die vorhergesagte abhängige Variable.,
Endergebnis: R-Squared = 0.6410828
Nehmen wir an, Sie haben in diesem Fall drei unabhängige Variablen.
n = 10
p = 3
adj.r.squared = 1 – (1 – R. squared) * ((n – 1)/(n-p-1))
print(adj.r.squared)
In diesem Fall, adjusted r-squared-Wert ist 0.4616242 angenommen, wir haben 3 Prädiktoren und 10 Beobachtungen.