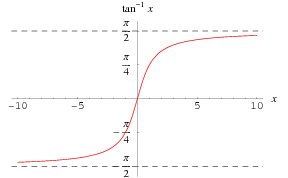
A inversa da função tangente 
é plotado acima ao longo do eixo real.
Pior ainda, a notação 
é usado às vezes para o valor principal, com 
sendo usado para a função multivalorada (Abramowitz e Stegun, 1972, p. 80)., Note that in the notation 
(commonly used in North America and in pocket calculators worldwide), 
denotes the tangent and 
the inverse function, not the multiplicative inverse.
O valor principal da tangente inversa é implementado como ArcTan na Linguagem Wolfram. Na biblioteca GNU C, Ela é implementada como atan(double x).,
a tangente inversa é uma função multivaluada e, portanto, requer um corte de ramo no plano complexo, que a Convenção da linguagem Wolfram coloca em 
e 
., Isto segue da definição de 
 |
(1)
|
No Wolfram da Linguagem (e, nesse trabalho), este ramo de corte definição determina o intervalo de 
real 
. Deve ter-se cuidado, no entanto, como outras definições de corte de ramo podem dar diferentes gamas (mais comumente, 
).,
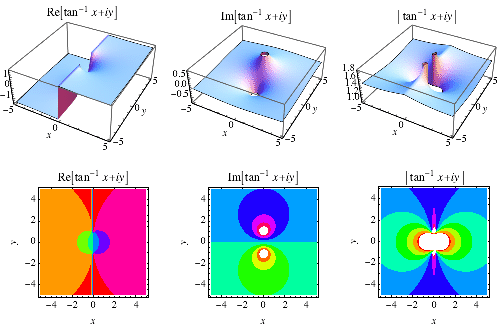
a função tangente inversa 
é plotada acima no plano complexo.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
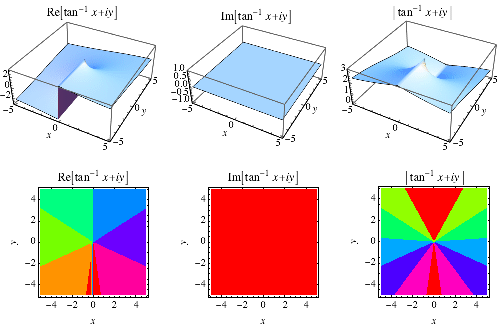
and 
. Plots of 
are illustrated above for real values of 
and 
.,
Um tipo especial de inversa da tangente, que leva em conta o quadrante em que 
mentiras e é retornado pelo comando FORTRAN ATAN2(y, x), a biblioteca GNU C comando atan2(double y, double x), e o Wolfram Linguagem de comando ArcTan, e é muitas vezes restrita ao intervalo 
.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
To find
numerically, the following arithmetic-geometric mean-like algorithm can be used.,464e247ac”>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
é redutível iff todos os fatores primos de 
ocorrer entre os fatores primos de 
para 
…, 
. A second necessary and sufficient condition is that the largest prime factor of 
is less than 
., Equivalente à segunda condição é a afirmação de que cada Gregory número 
pode ser unicamente expresso como uma soma em termos de 
que 
é um Størmer número (Conway e Cara 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway e Guy (1996) apresentam uma tabela semelhante em termos de números de Størmer.,
the finding one of which is a given as a problem by Bailey et al., (2006, p. 225).