|
Exponencial de Crescimento e Decadência
MathBitsNotebook.com Tópica de estrutura de tópicos | Álgebra 2 de estrutura de tópicos | MathBits’ Recursos do Professor Termos de Uso Pessoa de Contato: Donna Roberts |
Em Álgebra 1, a seguinte função de dois fórmulas foram usadas para ilustrar facilmente os conceitos de crescimento e decadência no aplicadas situações., Se uma quantidade cresce por uma porcentagem fixa em intervalos regulares, o padrão pode ser representado por estas funções.
|
Crescimento Exponencial:
y = a(1 + r)x |
Exponencial de Decaimento:
y = a(1 – r)x |
Lembre-se de que o original exponencial da fórmula y = abx.
você vai notar que nestas novas funções de crescimento e decaimento, o valor b (fator de crescimento) foi substituído por (1 + r) ou por (1 – r).,
O crescimento de uma “taxa” (r) é determinado como b = 1 + r.
A decadência de uma “taxa” (r) é determinado como b = 1 – r
r = o crescimento ou a taxa de decaimento (mais freqüentemente representado como um percentual expresso como um valor decimal)
x = número de intervalos de tempo que tem passado
Exemplo 1: A população da Cidade é de 2016 foi estimado em 35.000 pessoas, com uma taxa anual de crescimento de 2,4%.
a) qual é o Fator de crescimento para HomeTown?após um ano, a população seria de 35.000 + 0,024 (35000).,por factoring, temos 35000 (1 + 0.024) ou 35000(1.024).
O fator de crescimento é 1.024. (Lembre-se que o Fator de crescimento é maior que 1.)
|
b) escrever uma equação para modelar o crescimento futuro.
y = abx = a(1.014)x = 35000(1.024)x c) usar a equação para estimar a população em 2020 para as cem pessoas mais próximas. |
 |
![]()
a Maior parte dos fenômenos que ocorrem naturalmente a crescer continuamente. Por exemplo, as bactérias continuarão a crescer ao longo de um período de 24 horas, produzindo novas bactérias que também irão crescer. As bactérias não esperam até ao fim das 24 horas, e depois reproduzem-se todas ao mesmo tempo.
O exponencial e é usado na modelagem do crescimento contínuo que ocorre naturalmente, tais como populações, bactérias, decaimento radioativo, etc., Você pode pensar em e como uma constante universal representando o quão rápido você poderia crescer usando um processo contínuo. E, a beleza de e é que não só é usado para representar crescimento contínuo, mas também pode representar crescimento medido periodicamente ao longo do tempo (como o crescimento no exemplo 1).
na Álgebra 2, o exponencial e será usado em situações de crescimento contínuo ou decaimento. A seguinte fórmula é usada para ilustrar o crescimento contínuo e a decadência. Se uma quantidade cresce continuamente por uma porcentagem fixa, o padrão pode ser representado por esta função.,
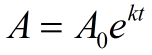
A0 = valor inicial (valor antes de medir o crescimento ou decaimento)
e = exponencial e = 2.71828183…,
k = contínuo taxa de crescimento (também chamado de constante de proporcionalidade)
(k > 0, a quantidade está aumentando (crescente); k < 0, o valor é decrescente (em decomposição))
t = tempo decorrido
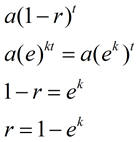 |
Se a gente comparar esta nova fórmula para o nosso antigo exponencial de decaimento fórmula (ou fórmula de crescimento), podemos ver como ek é relacionada com a taxa de decaimento, r, (ou de crescimento)., |
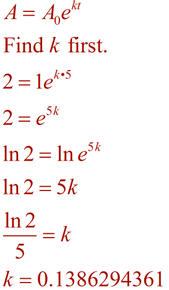 |
Agora, a forma da equação usando este valor de k, e resolver o problema usando o tempo de 96 minutos.,
|
![]()