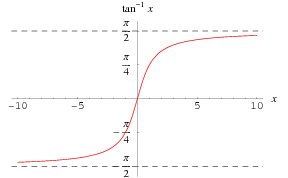
invers tangens-funksjonen 
er plottet over langs den reelle aksen.
enda Verre, notasjonen 
er noen ganger brukt for den viktigste verdien, med 
brukes for multivalued funksjon (Abramowitz og Stegun 1972, s. 80)., Merk at i notasjonen 
(ofte brukt i Nord-Amerika og i lommeregnere over hele verden), 
betegner tangent og 
den inverse funksjonen, ikke multiplicative omvendt.
Den viktigste verdien av invers tangens er implementert som ArcTan i Wolfram Språk. I GNU C library, det er implementert som atan(double x).,
invers tangens er en multivalued funksjon og derfor krever en gren skjæres i det komplekse planet, som Wolfram Språk-konvensjonen steder på 
og 
., Dette følger av definisjonen av 
som
 |
(1)
|
I Wolfram Språk (og i dette arbeidet), denne grenen kuttet definisjon bestemmer omfanget av 
for ekte 
som 
. Hensyn må tas, men som andre grenen kuttet definisjoner kan gi forskjellige områder (vanligvis 
).,
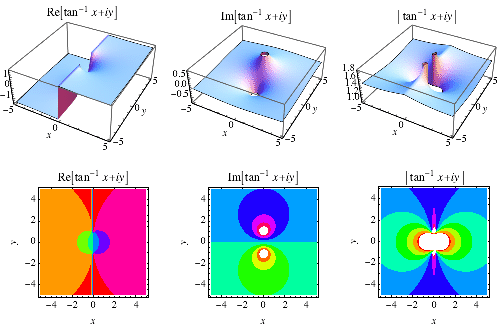
invers tangens-funksjonen 
er plottet over i det komplekse planet.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
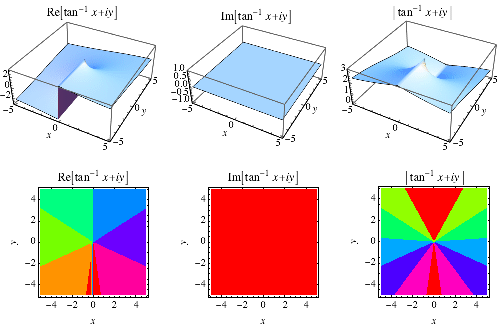
and 
. Plots of 
are illustrated above for real values of 
and 
.,
En spesiell type invers tangens som tar hensyn til kvadrant 
løgner og returneres av FORTRAN-kommandoen ATAN2(y, x), GNU C library kommando atan2(double y, double x), og Wolfram Språk ArcTan, og ofte er begrenset til rekkevidden 
.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
for Å finne 
numerisk, følgende aritmetiske-geometriske gjennomsnitt-algoritme som kan brukes.,464e247ac»>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
– er som kan reduseres iff alle prime faktorer av 
forekomme blant de førsteklasses faktorer av 
for 
, …, 
. En annen nødvendig og tilstrekkelig betingelse er at den største prime faktor av 
er mindre enn 
., Tilsvarende det andre vilkåret er uttalelsen som hver Gregory antall 
kan være unikt uttrykkes som en sum i form av 
s som 
er et Holding-nummer (Conway og Fyr 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway og Guy (1996) gir en tilsvarende tabell i form av Holding tall.,
the finding one of which is a given as a problem by Bailey et al., (2006, s. 225).