|
Eksponentiell Vekst og Forfall
MathBitsNotebook.com Aktuell Skissere | Algebra 2 Skissere | MathBits’ lærerressurser Vilkår for Bruk kontaktperson: Donna Roberts |
I Algebra 1, de to følgende funksjon formler ble brukt til å enkelt illustrere begrepene vekst og forfall i anvendt situasjoner., Hvis antallet øker med en fast prosent i regelmessige intervaller, mønsteret kan bli avbildet av disse funksjonene.
|
Eksponentiell Vekst:
y = a(1 + r)x |
Combine:
y = a(1 – r)x |
Husk at den opprinnelige eksponentiell formelen var y = abx.
vil Du legge merke til at i disse nye vekst og forfall, funksjoner,
b-verdi (vekstfaktor) har blitt erstattet enten ved (1 + r) eller av (1 – r).,
vekst «pris» (r) bestemmes som b = 1 + r.
forfall «pris» (r) bestemmes som b = 1 – r
r = vekst eller forfall pris (oftest representert som en prosentandel og uttrykt som et desimaltall)
x = antall tidsintervaller som har bestått
Eksempel 1: Befolkningen i Hjembyen er 2016 ble anslått til å være 35.000 mennesker med en årlig rate på økning på 2,4%.
a) Hva er vekst faktor for Hjemby?
Etter ett år i befolkningen ville være 35,000 + 0.024(35000).,
Ved factoring, har vi 35000(1 + 0.024) eller 35000(1.024).
growth factor er 1.024. (Husk at growth factor er større enn 1.)
|
b) Skriv en ligning til modell for fremtidig vekst.
y = abx = a(1.014)x = 35000(1.024)x c) Bruk formelen til å beregne befolkningen i 2020 til nærmeste hundre mennesker. |
 |
![]()
de Fleste naturlig forekommende fenomener vokse kontinuerlig. For eksempel bakterier vil fortsette å vokse over en 24 timers periode, produsere nye bakterier som også vil vokse. Bakterier trenger ikke vente til slutten av 24 timer, og deretter alle gjengi på en gang.
Den eksponentielle e) brukes når modellering kontinuerlig vekst som forekommer naturlig, for eksempel bestander, bakterier, radioaktive forfall, etc., Du kan tenke deg av e som en universell konstant representerer hvor fort du kan muligens vokse ved hjelp av en kontinuerlig prosess. Og, skjønnhet e er at ikke bare er det som brukes til å representere kontinuerlig vekst, men det kan også representere vekst målt med jevne mellomrom over tid (for eksempel veksten i Eksempel 1).
I Algebra 2, den eksponentielle e vil bli brukt i situasjoner med kontinuerlig vekst eller forfall. Følgende formel brukes for å illustrere kontinuerlig vekst og forfall. Hvis en mengde vokser kontinuerlig med en fast prosent, mønsteret kan være avbildet med denne funksjonen.,
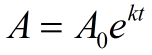
A0 = initial verdi (beløpet før måling av vekst eller forfall)
e = eksponentiell e = 2.71828183…,
k = kontinuerlig vekstrate (også kalt konstant om forholdsmessighet)
(k > 0, mengden er økende (økende); k < 0, beløpet er synkende (råtnende))
t = tid som har gått
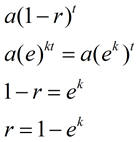 |
Hvis vi sammenligner denne nye formelen til våre tidligere combine formel (eller vekst formel), vi kan se hvordan ek er relatert til pris av forfall, r, (eller vekst)., |
(bakterier vokse kontinuerlig)
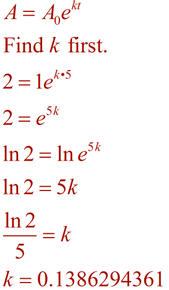 |
Nå, form ligningen ved hjelp av k-verdi, og løse problemet ved å bruke tid på 96 minutter.,
|
![]()