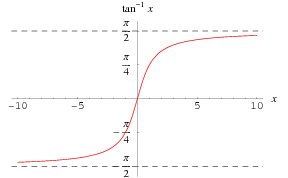
Die inverse Tangente Funktion 
ist oben entlang der reellen Achse aufgetragen.
Schlimmer noch, die Notation 
wird manchmal für den Hauptwert verwendet, wobei 
für die mehrwertige Funktion verwendet wird (Abramowitz und Stegun 1972, S. 80)., Beachten Sie, dass in der Notation 
(häufig in Nordamerika und in Taschenrechnern weltweit verwendet) 
bezeichnet die Tangente und die inverse Funktion, nicht die multiplikative Inverse.
Der Hauptwert der inversen Tangente wird in der Wolfram-Sprache als ArcTan implementiert. In der GNU C-Bibliothek ist es als atan(double x) implementiert.,
Die inverse Tangente ist eine mehrwertige Funktion und erfordert daher einen Verzweigungsschnitt in der komplexen Ebene, den die Wolfram Language ‚ s convention bei 
und 
platziert., Dies ergibt sich aus der Definition von 
als
|
(1)
|
In der Wolfram-Sprache (und in dieser Arbeit) bestimmt diese Verzweigungsschnittdefinition den Bereich von 
für echte 
als 
. Es ist jedoch Vorsicht geboten, da andere Verzweigungsschnittdefinitionen unterschiedliche Bereiche angeben können (am häufigsten 
).,
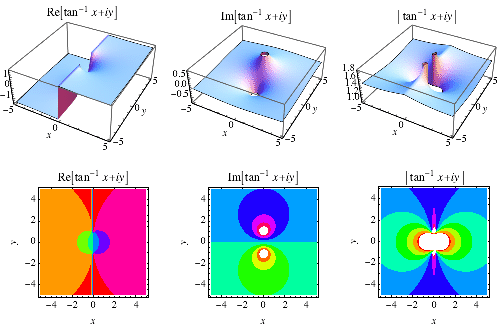
Die inverse Tangensenfunktion 
ist oben in der komplexen Ebene aufgetragen.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
and 
. Plots of 
are illustrated above for real values of 
and 
.,
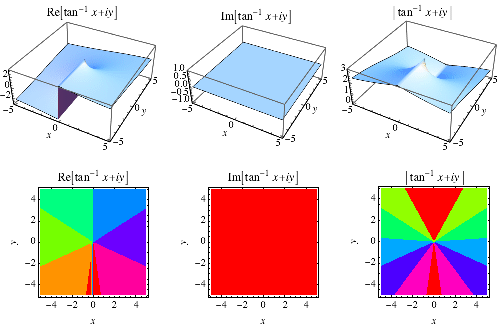
Eine spezielle Art von inverser Tangente, die den Quadranten berücksichtigt, in dem 
liegt und vom FORTRAN-Befehl ATAN2(y, x), dem GNU C-Bibliotheksbefehl atan2(double y, double x) und dem Wolfram-Sprachbefehl ArcTan zurückgegeben wird und häufig auf den Bereich beschränkt ist 
.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
Um 
numerisch zu finden, kann der folgende arithmetisch-geometrische Mittelalgorithmus verwendet werden.,464e247ac“>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
ist reduzierbar, wenn alle Primfaktoren von 
unter den Primfaktoren von 
für 
auftreten …, 
. Eine zweite notwendige und ausreichende Bedingung ist, dass der größte Primfaktor von 
kleiner ist als 
., Entsprechend der zweiten Bedingung ist die Aussage, dass jede einzelne Zahl 
eindeutig als Summe in Form von 
s ausgedrückt werden kann, für die 
eine Størmer-Zahl ist (Conway und Guy 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway und Guy (1996) geben eine ähnliche Tabelle in Bezug auf die Størmer-zahlen.,
the finding one of which is a given as a problem by Bailey et al., (2006, S. 225).