|
What is the Origami Cube?,
… |
origami cube on kuutio voit taittaa alkaen squaresheet paperia.
toinen nimi on vesipommi. |
Taitto theOrigami Cubetop
1
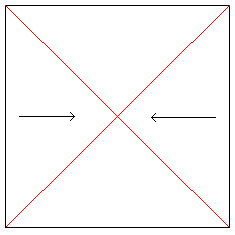 |
Taita neliön arkin lävistäjät ja unfoldit.
laita paperi molempiin nuoliin yhteen. |
2
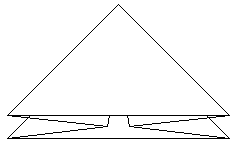 |
The result is a flier triangle, which is known from theswallow or the pigeon. |
3
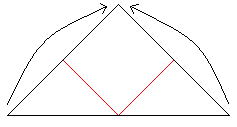 |
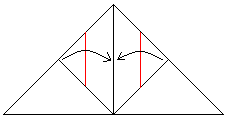
Fold upward on the red line on the right and on the left., |
4
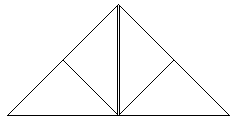 |
Then it must look like this. |
5
 |
Fold on the red lines., |
6
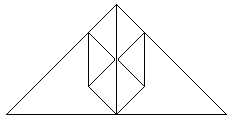 |
Then it must look like this. |
7
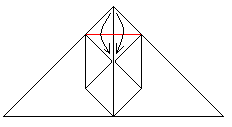 |
Fold the two little triangles on the red lines downward., |
8
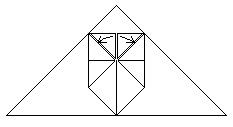 |
Put the last made triangles in the two pockets on theright and on the left. This is a little bit fiddly. |
9
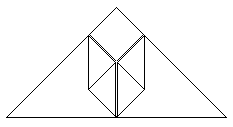 |
Then it must look like this., |
10
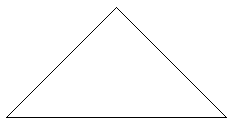 |
Turn the whole triangle and repeat the steps 3,4,5,6,7,8,9. |
11
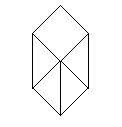 |
Then it must look like this., |
12
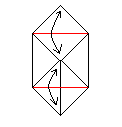 |
Fold and unfold on the red lines. |
13
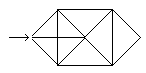 |
Take the folded cube in hand and blow into the hole atthe top. Unfold the cube by this., |
14
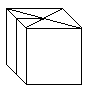 |
finished |
Some Mathematics top
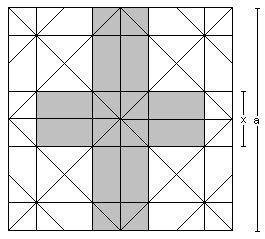 |
If you take the cube apart, you get a nice pattern, whichis made by the folds.
You find the formulas: ………, |
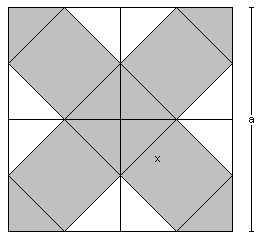 |
vasemmalla näet kuution suurimman verkon, joka on neliö.
Voit löytää kaavoja:
Tämä kuutio on paljon suurempi kuin taitettu kuutio., |
Jos haluat käyttää kuution koko neliötä, olet formula_3
tämä on teoriassa suurin kuutio.
Katso lisää kirjasta (5), sivulta 63f ja sivulta 71ff. Dereingewickelte Würfel (S.
OrigamiCube Internetissä
Englisch
Dr Stephen O ’ hanlon (Rengas Origami Art)
WaterBomb ( .,pdf-tiedosto)
Gerwin Sturm (Origami kaikille)
Waterbomb
Puzzle Playground (Puzzle_com)
Squareto Cube
Wikipedia
Waterballoon
Englanti
Jennifer ’ sPuzzle
hauduttaa 3 liuskan
Umwelthaus Pinneberg e. V.,
Wasserbombeaus paperi
Wikipedia
vesi pommi(lelu)
zzzebra
vesi pommi
Viitteet alkuun
(1) Joachim Schönherr, Me taita ja taitto, Leipzig1990
(2) Therese Mielhaht: Origami hauskaa paperin taitto,Köln, 1990
(3) Kunihiko Kasahara Origami kuvio-ja geometrinen,München, 2000
(4) Kunihiko Kasahara Origami ilman rajoja, München2001
(5) Martin Gardner: Matemaattinen noituus, Berliini/frankfurtammain/Wien 1988