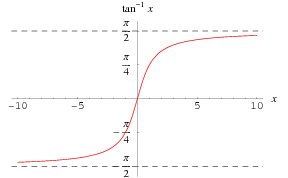
inverse tangentti toiminto 
on piirretty edellä pitkin oikea-akselilla.
vielä Pahempaa, merkintä 
käytetään joskus pääasiallinen arvo, jossa 
käytetään multivalued toiminto (Abramowitz ja Stegun 1972, s. 80)., Huomaa, että merkintä 
(yleisesti käytetty Pohjois-Amerikassa ja taskulaskimet maailmanlaajuisesti), 
tarkoittaa tangentin ja 
käänteinen toiminto, ei multiplicative käänteinen.
käänteisen tangentin pääarvo toteutetaan Arctanina Wolframin kielellä. GNU C-kirjastossa se toteutetaan nimellä atan (double x).,
inverse tangentti on multivalued toiminto ja näin ollen vaatii haara leikataan monimutkainen kone, joka Wolfram Kielellä on yleissopimuksen paikassa 
ja 
., Tämä seuraa määritelmästä 
kuin
 |
(1)
|
Wolfram Kielellä (ja tässä työssä), tämä haara leikataan määritelmä määrittää valikoima 
todellinen 
kuten 
. Varovaisuutta on kuitenkin noudatettava, sillä muut haaran leikkausmääritelmät voivat antaa erilaisia vaihteluvälejä (yleisimmin 
).,
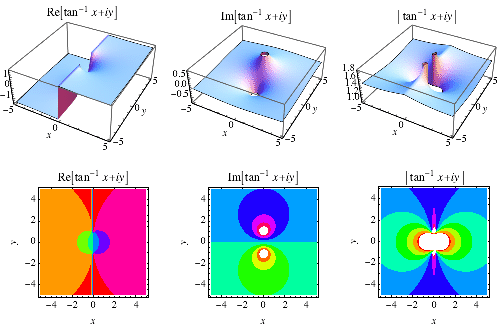
inverse tangentti toiminto 
on piirretty edellä monimutkainen kone.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
and 
. Plots of 
are illustrated above for real values of 
and 
.,
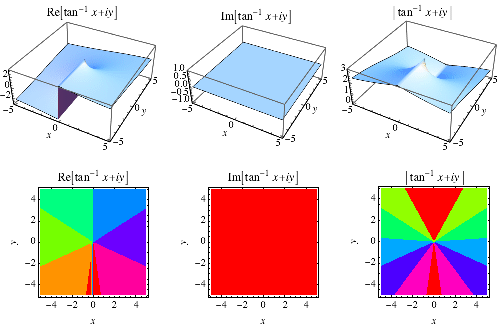
erikoinen inverse tangentti, joka ottaa huomioon quadrant, jossa 
valheita ja palauttaa FORTRAN komento ATAN2(y, x), GNU C-kirjasto komento atan2(double y, double x), ja Wolfram Kielellä komento ArcTan, ja on usein rajoitettu valikoima 
.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
löytää 
numeerisesti, seuraavat aritmeettinen-geometrinen keskiarvo-algoritmia voidaan käyttää.,464e247ac”>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
on pelkistettävissä iff kaikki prime tekijät 
esiintyy joukossa prime tekijät 
for 
, …, 
. Toinen välttämätön ja riittävä ehto on, että suurin prime tekijä 
alle 
., Vastaa toinen edellytys on selvitys siitä, että jokainen Gregory numero 
voi olla yksiselitteisesti ilmaistu summa suhteen 
s, josta 
on Størmer numero (Conway ja Kaveri 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway ja Guy (1996) antavat samanlaisen taulukon størmer-lukujen suhteen.,
the finding one of which is a given as a problem by Bailey et al., (2006, s. 225.