Ero Adjusted R-squared ja R-squared

T-neliö (R2)
Se mittaa osuus vaihtelua omalla riippuva muuttuja selittää kaikki riippumattomat muuttujat mallissa. Se olettaa, että jokainen riippumaton muuttuja mallissa auttaa selittämään vaihtelua riippuvainen muuttuja., Todellisuudessa jotkut riippumattomat muuttujat (prediktorit) eivät auta selittämään riippuvaista (target) muuttujaa. Toisin sanoen jotkin muuttujat eivät edistä tavoitemuuttujan ennustamista.
matemaattisesti R-neliö lasketaan jakamalla jäännösten (SSres) neliöiden summa neliösummalla (sstot) ja vähennetään se sitten 1. Tällöin SStot mittaa kokonaisvaihtelua. SSreg toimenpiteet selitti vaihtelua ja SSres toimenpiteet selittämätön vaihtelu.,
as SSres + SSreg = SStot, R2=selitetty variaatio / Kokonaisvaihtelu

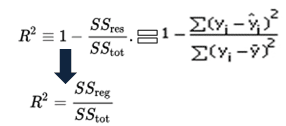
r-neliöinen yhtälö

R-neliöinen on myös määrityskerroin. Se on 0-100 prosenttia. R-squared arvo 100% tarkoittaa, että malli selittää vaihtelua kohde-muuttuja. Ja arvo 0% mittaa mallin Nollaa ennustavaa tehoa. Korkeampi R-neliöinen arvo, parempi malli.
korjattu R-neliö
se mittaa vaihtelun osuutta, joka selittyy vain niillä riippumattomilla muuttujilla, jotka todella auttavat selittämään riippuvaista muuttujaa., Se rankaisee sinua lisäämällä riippumaton muuttuja, jotka eivät auta ennustaa riippuvainen muuttuja.
oikaistu R-neliö voidaan laskea matemaattisesti neliöiden summana. Ainoa ero R-neliön ja oikaistun R-neliöyhtälön välillä on vapausaste.

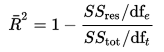
oikaistu R-neliöinen yhtälö

edellä mainitussa yhtälössä DFT on riippuvan muuttujan populaatiovarianssin estimaatin vapausaste n– 1, ja dfe on taustalla olevan väestövirhevarianssin estimaatin vapausaste N – p – 1.,
korjattu R-neliöarvo voidaan laskea R-neliöisen arvon, riippumattomien muuttujien lukumäärän (prediktorien), kokonaisnäytteen koon perusteella.

Adjusted R-Squared Yhtälö 2

Ero R-square ja Säätää R-square

1. Joka kerta, kun lisäät riippumaton muuttuja malli, R-squared lisää, vaikka riippumaton muuttuja on merkityksetön. Se ei koskaan laske. Kun taas mukautettu R-neliö kasvaa vain silloin, kun itsenäinen muuttuja on merkittävä ja vaikuttaa riippuvaiseen muuttujaan.,

alla olevassa taulukossa korjattu R-neliö on maksimi, kun mukaan otettiin kaksi muuttujaa. Se laskee, kun lisätään kolmas muuttuja. Kun taas R-neliö kasvaa, kun sisällytimme kolmannen muuttujan. Se tarkoittaa, että kolmas muuttuja on mallille merkityksetön.



T-Neliö vs. Adjusted R-Squared

2. Adjusted r-squared voi olla negatiivinen, kun r-squared on lähellä nollaa.
3. korjattu R-neliöarvo on aina pienempi tai yhtä suuri kuin r-neliöinen arvo.

oikaistua R-neliötä tulee käyttää mallien vertailuun eri määrä riippumattomia muuttujia. Regressiomallin tärkeitä ennustimia (itsenäisiä muuttujia) valittaessa on käytettävä oikaistua R-neliötä.

R : Laske R: n ja Adjusted R-Squared
Oletetaan, että sinulla on todellinen ja ennustaa riippuvan muuttujan arvoja. Alla olevassa käsikirjoituksessa olemme luoneet otoksen näistä arvoista. Tässä esimerkissä y tarkoittaa havaittua riippuvaista muuttujaa ja yhat viittaa ennustettuun riippuvaiseen muuttujaan.,
lopputulos: R-Squared = 0,6410828
oletetaan, että tässä tapauksessa on kolme itsenäistä muuttujaa.

n = 10
p = 3
adj.R.squared = 1 – (1 – R. squared) * ((n – 1)/(n-p-1)))
print(adj.R.squared)

tässä tapauksessa korjattu R-squared arvo on 0.4616242 olettaen, että meillä on 3 predikaattoria ja 10 havaintoa.

Python : Laskea, Adjusted R-Squared ja R-Squared