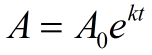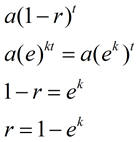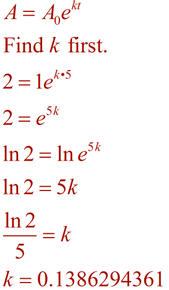|
Eksponentiaalinen Kasvu ja Rappeutuminen MathBitsNotebook.com Ajankohtainen Ääriviivat | Algebra 2 Ääriviivat | MathBits’ Opettaja Resursseja Käyttöehdot Yhteyshenkilö: Donna Roberts  |
Algebra 1, seuraavat kaksi toimintoa kaavoja käytettiin helposti kuvaavat käsitteet kasvu ja rappeutuminen soveltaa tilanteissa., Jos määrä kasvaa kiinteällä prosentilla säännöllisin väliajoin, kuvio voidaan kuvata näillä funktioilla.
|
eksponentiaalinen kasvu:
y = a(1 + r)x
|
eksponentiaalinen hajoaminen:
y = a(1 – R)x
|
muista, että alkuperäinen eksponentiaalinen kaava oli y = ABX.
huomaat, että nämä uudet kasvu ja rappeutuminen toimintoja,
b arvo (kasvutekijä) on korvattu joko (1 + r) tai (1 – r).,
kasvu ”korko” (r) määritellään b = 1 + r.
rappeutuminen ”korko” (r) määritellään b = 1 – r –
a = alustava arvo (määrä ennen mittausta kasvua tai rappeutuminen)
r = kasvua tai rappeutuminen korko (useimmiten edustettuna prosentteina ja ilmaisi desimaalin)
x = määrä aikavälejä, jotka ovat läpäisseet
Esimerkki 1: Väestö Kotikaupunki on 2016 oli arviolta 35 000 ihmistä, joiden vuotuinen kasvuvauhti oli 2,4 prosenttia.
a) mikä on kotikaupungin kasvutekijä?
vuoden kuluttua väkiluku olisi 35 000 + 0,024(35 000).,
factoringin mukaan meillä on 35000(1 + 0,024) tai 35000 (1,024).
kasvutekijä on 1,024. (Muista, että kasvutekijä on suurempi kuin 1.)
|
b) Kirjoita yhtälö mallintaa tulevaa kasvua.
y = abx = a(1, 014)x = 35000 (1, 024)x
c) käyttää yhtälöä arvioidakseen asukasluvun vuonna 2020 lähimmälle sadalle ihmiselle.
y = 35000 (1, 024)4 ≈ 38, 482.,91 ≈ 38 500
|
|
useimmat luonnossa esiintyvät ilmiöt kasvavat jatkuvasti. Esimerkiksi bakteerit jatkavat kasvuaan 24 tunnin ajan, jolloin syntyy uusia bakteereja,jotka myös kasvavat. Bakteerit eivät odota 24 tunnin loppuun, ja sitten kaikki lisääntyvät kerralla.
eksponentiaalista e: tä käytetään mallinnettaessa luonnossa esiintyvää jatkuvaa kasvua, kuten populaatioita, bakteereita, radioaktiivista hajoamista jne., Voit ajatella E kuin universaali vakio edustaa kuinka nopeasti voit mahdollisesti kasvaa käyttämällä jatkuvaa prosessia. Ja, kauneus e on, että ei vain se käytetään edustamaan jatkuva kasvu, mutta se voi myös edustaa kasvua mitataan säännöllisesti koko ajan (kuten kasvu, Esimerkki 1).
Algebra 2, eksponentti-e käytetään tilanteissa, jatkuva kasvu tai rappeutuminen. Seuraavaa kaavaa käytetään kuvaamaan jatkuvaa kasvua ja hajoamista. Jos määrä kasvaa jatkuvasti kiinteällä prosentilla, kuviota voidaan kuvata tällä funktiolla.,
jatkuva eksponentiaalinen kasvu tai hajoaminen
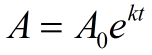
a = loppuarvo (määrä kasvun tai hajoamisen jälkeen)
A0 = alkuarvo (määrä ennen kasvun tai hajoamisen mittaamista)
e = eksponentiaalinen e = 2,71828183…,
k = jatkuva kasvu (kutsutaan myös vakio suhteellisuusperiaate)
(k > 0, määrä kasvaa (kasvaa); k < 0, määrä on laskussa (rappeutunut))
t = aika, joka on kulunut
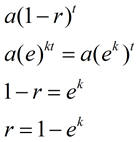 |
Jos vertaamme tämän uuden kaavan edellisessä eksponentiaalinen hajoaminen kaava (tai kasvun kaava), voimme nähdä, kuinka ek on liittyvät määrä rappeutuminen, r, (tai kasvua)., |
esimerkki: työpöydälläsi kasvava bakteerikanta kaksinkertaistuu 5 minuutin välein. Olettaen, että aloitat vain yhdellä bakteerilla, kuinka monta bakteeria voi olla läsnä 96 minuutin kuluttua?
(bakteerit kasvavat jatkuvasti)
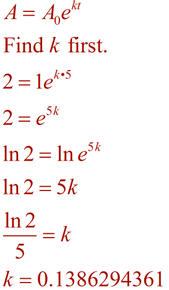 |
nyt muodostakaa yhtälö käyttäen tätä k-arvoa, ja ratkaista ongelman käyttämällä aikaa 96 minuuttia.,
|



![]()