|
Exponentielles Wachstum und Zerfall
MathBitsNotebook.com Topical Outline / Algebra 2 Outline / MathBits ‚Teacher Resources Nutzungsbedingungen Ansprechpartner: Donna Roberts |
In Algebra 1 wurden die folgenden zwei Funktionsformeln verwendet, um die Konzepte von Wachstum und Verfall in angewandten Situationen leicht zu veranschaulichen., Wenn eine Menge in regelmäßigen Abständen um einen festen Prozentsatz wächst, kann das Muster durch diese Funktionen dargestellt werden.
|
Exponentielles Wachstum:
y = a(1 + r)x |
Exponentiellen Zerfall:
y = a(1 – r)x |
denken Sie Daran, dass die original exponentielle Formel y = abx.
Sie werden feststellen, dass in dieser neuen Wachstum und Zerfall Funktionen,
die b-Wert (growth factor) wurde ersetzt-entweder durch (1 + r) – oder (1 – r).,
Die Wachstumsrate „rate“ (r) wird als b = 1 + r bestimmt.
Die Zerfallsrate „rate“ (r) wird als b = 1 – r bestimmt
r = Wachstums-oder Zerfallsrate (am häufigsten als Prozentsatz dargestellt und als Dezimalzahl ausgedrückt)
x = Anzahl der Zeitintervalle, die vergangen sind
Beispiel 1: Die Bevölkerung der Heimatstadt wird auf 35.000 Menschen geschätzt.mit einer jährlichen Steigerungsrate von 2,4%.
a) Was ist der Wachstumsfaktor für Heimatstadt?
Nach einem Jahr wäre die Bevölkerung 35.000 + 0.024 (35000).,
Durch Factoring haben wir 35000(1 + 0.024) oder 35000 (1.024).
Der Wachstumsfaktor ist 1.024. (Denken Sie daran, dass der Wachstumsfaktor größer als 1 ist.)
|
b) Schreiben Sie eine Gleichung, um das Modell das zukünftige Wachstum.
y = abx = a(1.014)x = 35000 (1.024)x c) Verwenden Sie die Gleichung, um die Bevölkerung im Jahr 2020 auf die nächsten hundert Personen zu schätzen. |
 |
![]()
die Meisten natürlich vorkommenden Phänomene, die kontinuierlich wachsen. Zum Beispiel werden Bakterien über einen Zeitraum von 24 Stunden weiter wachsen und neue Bakterien produzieren, die ebenfalls wachsen werden. Die Bakterien warten nicht bis zum Ende der 24 Stunden und dann vermehren sich alle auf einmal.
Das exponentielle e wird verwendet, um kontinuierliches Wachstum zu modellieren, das natürlich auftritt, wie Populationen, Bakterien, radioaktiver Zerfall usw., Sie können sich e wie eine universelle Konstante vorstellen, die darstellt, wie schnell Sie möglicherweise mit einem kontinuierlichen Prozess wachsen könnten. Das Schöne an e ist, dass es nicht nur verwendet wird, um ein kontinuierliches Wachstum darzustellen, sondern auch ein periodisch über die Zeit gemessenes Wachstum darstellen kann (wie das Wachstum in Beispiel 1).
In der Algebra 2 wird das exponentielle e in Situationen kontinuierlichen Wachstums oder Zerfalls verwendet. Die folgende Formel wird verwendet, um kontinuierliches Wachstum und Zerfall zu veranschaulichen. Wenn eine Menge kontinuierlich um ein festes Prozent wächst, kann das Muster durch diese Funktion dargestellt werden.,
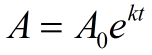
A0 = Anfangswert (Betrag vor Messung von Wachstum oder Verfall)
e = exponentielles e = 2.71828183…,
k = kontinuierliche Wachstumsrate (auch als Konstante der Proportionalität bezeichnet)
(k > 0, die Menge nimmt zu (wächst); k < 0, die Menge nimmt ab (Verfall))
t = Zeit, die vergangen ist
div>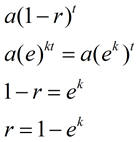 |
Wenn wir diese neue Formel mit unserer vorherigen exponentiellen Zerfallsformel (oder Wachstumsformel) vergleichen, können wir sehen, wie ek mit der Zerfallsrate, r (oder Wachstum) zusammenhängt., |
(Bakterien wachsen kontinuierlich)
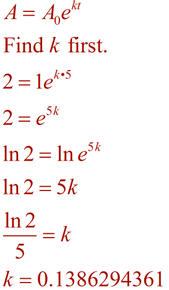 |
Bilden Sie nun die Gleichung mit diesem k-Wert und lösen Sie das Problem mit der Zeit von 96 Minuten.,
|
![]()