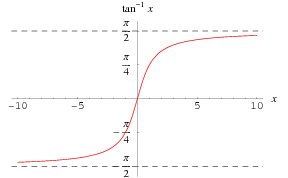
den inverse tangenten
tangent funktion 
ritas ovanför den verkliga axeln.
ännu värre, notationen 
används ibland för huvudvärdet, med 
används för multivalued-funktionen (Abramowitz och Stegun 1972, s. 80)., Observera att i notationen 
(vanligen används i Nordamerika och i pocket räknare över hela världen) betecknar 
tangenten och 
den inversa funktionen, inte den multiplikativa inversen.
huvudvärdet av den inverse tangenten implementeras som ArcTan på Wolfram-språket. I GNU C-biblioteket implementeras det som atan(double x).,
den inversa tangenten är en multivaluerad funktion och kräver därför en grenskärning i det komplexa planet, som Wolfram-språkets konvention placerar på 
och 
., Detta följer av definitionen av 
som
 |
(1)
|
i Wolfram-språket (och i det här arbetet) bestämmer den här grenskärningsdefinitionen intervallet 
på riktigt 
som 
. Försiktighet måste dock iakttas, eftersom andra grenskärningsdefinitioner kan ge olika intervall (oftast 
).,
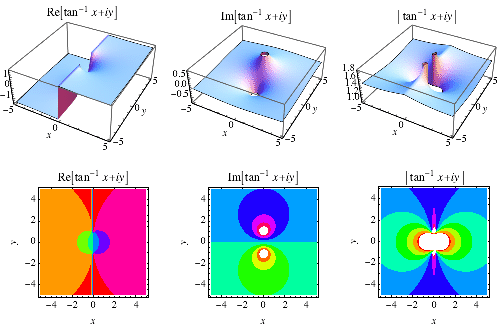
den inverse tangent funktionen
ritas ovan i det komplexa planet.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
and 
. Plots of 
are illustrated above for real values of 
and 
.,
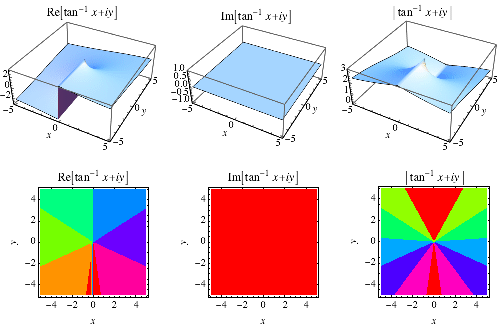
en speciell typ av omvänd tangent som tar hänsyn till kvadranten där 
ligger och returneras av FORTRAN-kommandot ATAN2(y, x), GNU C-bibliotekskommandot atan2(dubbel y, dubbel x) och Wolfram-Språkkommandot ArcTan, och är ofta begränsat till intervallet
.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
för att hitta
Numeriskt kan följande aritmetiska geometriska medelliknande algoritm användas.,464e247ac”>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
är reducerbar iff alla de viktigaste faktorerna för
förekommer bland de främsta faktorerna för
för
,…, 
. Ett andra nödvändigt och tillräckligt villkor är att den största huvudfaktorn för 
är mindre än 
., Motsvarande det andra villkoret är uttalandet att varje Gregory-nummer 
kan uttryckas unikt som en summa i form av 
s för vilka 
är ett Størmer-nummer (Conway och Guy 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway och Guy (1996) ger ett liknande bord när det gäller Størmer-nummer.,
the finding one of which is a given as a problem by Bailey et al., (2006, s. 225).