|
exponentiell tillväxt och förfall
MathBitsNotebook.com aktuell disposition | Algebra 2 disposition/MathBits lärarresurser Användarvillkor kontaktperson: Donna Roberts |
i Algebra 1 användes följande två funktionsformler för att enkelt illustrera begreppen tillväxt och förfall i tillämpade situationer., Om en kvantitet växer med en fast procent med jämna mellanrum kan mönstret avbildas av dessa funktioner.
|
exponentiell tillväxt:
y = a(1 + r)x |
exponentiell förfall:
y = a(1 – R)x |
kom ihåg att den ursprungliga exponentiella formeln var y = ABX.
Du kommer att märka att i dessa nya tillväxt – och sönderfallsfunktioner har
b-värdet (tillväxtfaktor) ersatts antingen av (1 + r) eller av (1-r).,
tillväxten ”rate” (r) bestäms som B = 1 + r.
sönderfallet ”rate” (r) bestäms som B = 1 – r
r = tillväxt eller sönderfallshastighet (oftast representerad som procentandel och uttryckt som decimal)
x = antal tidsintervaller som har passerat
exempel 1: befolkningen i hemstad uppskattas till 35 000 invånare.personer med en årlig ökning på 2,4%.
A) Vad är tillväxtfaktorn för hemstad?
efter ett år skulle befolkningen vara 35 000 + 0, 024(35000).,
genom factoring har vi 35000(1 + 0.024) eller 35000(1.024).
tillväxtfaktorn är 1, 024. (Kom ihåg att tillväxtfaktorn är större än 1.)
|
b) Skriv en ekvation för att modellera framtida tillväxt.
y = abx = a(1.014)x = 35000(1.024)x c) använd ekvationen för att uppskatta befolkningen 2020 till närmaste hundra personer. |
 |
![]()
de flesta naturligt förekommande fenomen växer kontinuerligt. Till exempel kommer bakterier att fortsätta att växa under en 24-timmarsperiod och producera nya bakterier som också kommer att växa. Bakterierna väntar inte till slutet av 24-timmarna, och sedan reproducerar alla på en gång.
exponentiell e används vid modellering av kontinuerlig tillväxt som uppträder naturligt som populationer, bakterier, radioaktivt sönderfall etc., Du kan tänka på e som en universell konstant representerar hur snabbt du skulle kunna växa med hjälp av en kontinuerlig process. Och skönheten i e är att det inte bara används för att representera kontinuerlig tillväxt, men det kan också representera tillväxt mätt periodiskt över tiden (till exempel tillväxten i Exempel 1).
i Algebra 2 kommer exponentiell e att användas i situationer med kontinuerlig tillväxt eller förfall. Följande formel används för att illustrera kontinuerlig tillväxt och förfall. Om en kvantitet växer kontinuerligt med en fast procent kan mönstret avbildas av denna funktion.,
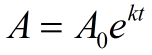
A0 = initialvärde (belopp före mätning av tillväxt eller förfall)
e = exponentiell e = 2.71828183…,
k = kontinuerlig tillväxt (även kallad konstant proportionalitet)
(k > 0, mängden ökar (växer); k < 0, mängden minskar (förfaller))
t = tid som har passerat
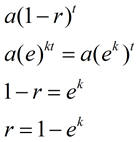 |
om vi jämför denna nya formel med vår tidigare exponentiella sönderfallsformel (eller tillväxtformel) kan vi se hur ek är relaterad till sönderfallshastigheten, r, (eller tillväxt)., |
(bakterier växer kontinuerligt)
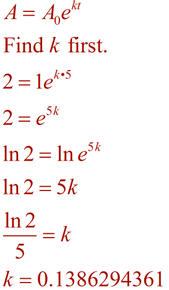 |
bilda nu ekvationen med detta k-värde och lösa problemet med tiden på 96 minuter.,
|
![]()