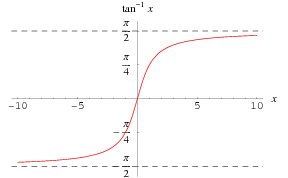
funcție inversă a funcției tangentă 
este reprezentată de mai sus de-a lungul axei reale.
mai Rău încă, notația 
este folosit uneori pentru valoarea principală, cu 
utilizat pentru multivoci funcția (Abramowitz și Stegun 1972, p. 80)., Rețineți că, în notația 
(utilizate în mod obișnuit în America de Nord și în calculatoare de buzunar din lume), 
reprezintă tangenta și 
funcția inversă, nu invers multiplicativ.valoarea principală a tangentei inverse este implementată ca ArcTan în limba Wolfram. În biblioteca GNU C, este implementat ca atan (double x).,
inversul tangentei este o funcție, funcția și, prin urmare, necesită o ramură tăiată în planul complex, care Wolfram Limba convenția de locuri la 
și 
., Acest lucru rezultă din definiția 
 |
(1)
|
În Wolfram Language (și în această lucrare), această ramură se taie definiție determină gama de 
pentru reali 
ca 
. Cu toate acestea, trebuie avut grijă, deoarece alte definiții de tăiere a ramurilor pot da diferite intervale (cel mai frecvent, 
).,
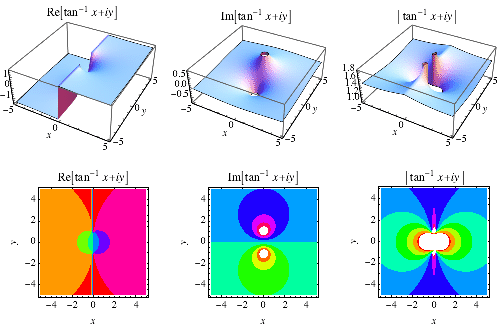
funcția tangentă inversă
este reprezentată mai sus în planul complex.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
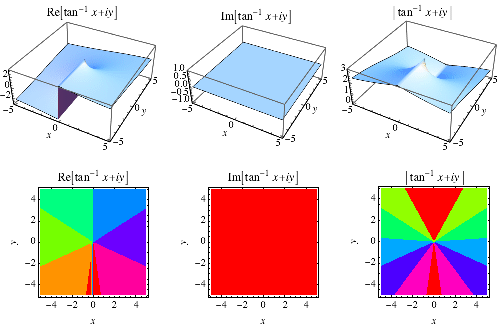
and 
. Plots of 
are illustrated above for real values of 
and 
.,
Un tip special de inverse tangent care să țină cont de cadranul în care 
minciuni și este returnat de FORTRAN comanda ATAN2(y, x), GNU C library comanda atan2(double y, double x), și Wolfram Limba comanda ArcTan, și este de multe ori limitată la intervalul 
.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
pentru a găsi 
numeric, se poate utiliza următorul algoritm aritmetic-geometric asemănător mediei.,464e247ac”>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
este reductibilă dacă toți factorii de prim 
apar printre factorii de prim 
pentru 
, …, 
. O a doua condiție necesară și suficientă este că cel mai mare factor prim al 
este mai mic decât 
., Echivalentă cu cea de-a doua condiție este declarația pe care fiecare Gregory numărul 
poate fi unic exprimată ca o sumă în termeni de 
– uri pentru care 
este un Størmer numărul (Conway și Tipul 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway și Guy (1996) oferă un tabel similar în ceea ce privește numerele Størmer.,
the finding one of which is a given as a problem by Bailey et al., (2006, p. 225).