|
Exponențială de Creștere și Decădere
MathBitsNotebook.com Actualitate Contur | Algebra 2 Outline | MathBits’ Profesor Resurse Termeni de Utilizare Persoană de Contact: Donna Roberts |
În Algebra 1, următoarele două funcții formule au fost folosite pentru a ilustra cu ușurință conceptele de creștere și decădere aplicate situații., Dacă o cantitate crește cu un procent fix la intervale regulate, modelul poate fi descris de aceste funcții.
|
Creștere Exponențială:
y = (1 + r)x |
Exponențială:
y = a(1 – r)x |
Amintiți-vă că originalul exponențială formula y = abx.
veți observa că în aceste noi funcții de creștere și degradare,
valoarea b (factorul de creștere) a fost înlocuită fie cu (1 + r), fie cu (1 – r).,
creșterea „rata” (r) se determină ca b = 1 + r.
degradare „rata” (r) se determină ca b = 1 – r
r = creștere sau rata de descompunere (cel mai adesea reprezentat ca un procent și exprimată ca zecimală)
x = numărul de intervale de timp care au trecut
Exemplu 1: Populația din orașul Natal este 2016 a fost estimată la 35.000 de oameni, cu o rată anuală de creștere de 2,4%.
A) care este factorul de creștere pentru orașul natal?
după un an populația ar fi 35,000 + 0.024 (35000).,
prin factoring, avem 35000(1 + 0.024) sau 35000 (1.024).
factorul de creștere este 1.024. (Amintiți-vă că factorul de creștere este mai mare decât 1.)
|
b) scrieți o ecuație pentru a modela creșterea viitoare.
y = abx = a(1.014)x = 35000 (1.024)x c) utilizați ecuația pentru a estima populația în 2020 la cele mai apropiate sute de persoane. |
 |
![]()
cele Mai multe fenomene care apar în mod natural să crească continuu. De exemplu, bacteriile vor continua să crească pe o perioadă de 24 de ore, producând noi bacterii care vor crește și ele. Bacteriile nu așteaptă până la sfârșitul celor 24 de ore și apoi se reproduc imediat.
E exponențial este utilizat atunci când se modelează o creștere continuă care apare în mod natural, cum ar fi populațiile, bacteriile, dezintegrarea radioactivă etc., Vă puteți gândi la e ca la o constantă universală reprezentând cât de repede ați putea crește folosind un proces continuu. Și frumusețea e este că nu numai că este folosită pentru a reprezenta o creștere continuă, dar poate reprezenta și o creștere măsurată periodic de-a lungul timpului (cum ar fi creșterea din exemplul 1).în Algebra 2, exponențialul e va fi utilizat în situații de creștere continuă sau degradare. Următoarea formulă este utilizată pentru a ilustra creșterea și degradarea continuă. Dacă o cantitate crește continuu cu un procent fix, modelul poate fi descris de această funcție.,
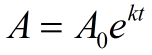
A0 = valoarea inițială (sumă înainte de măsurarea creșterii sau degradare)
e = exponențială e = 2.71828183…,
k = rata de creștere continuă (de asemenea, numit constantă de proporționalitate)
(k > 0, suma este în creștere (în creștere); k < 0, suma este în scădere (descompunere))
t = timpul care a trecut
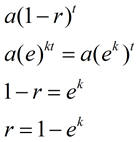 |
Dacă vom compara această nouă formulă noastre anterioare exponențială formula (sau formula de creștere), putem vedea cum ek este legat de rata de degradare, r, (sau de creștere)., |
(bacterii crește în mod continuu)
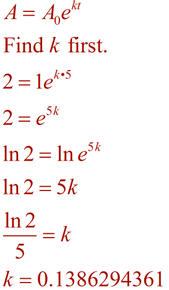 |
Acum, forma ecuației folosind această valoare k, și de a rezolva problema folosind timp de 96 de minute.,
|
![]()