R-pătrat (R2)
acesta măsoară proporția variației variabilei dependente explicată de toate variabilele independente din model. Se presupune că fiecare variabilă independentă din model ajută la explicarea variației variabilei dependente., În realitate, unele variabile independente (predictori) nu ajută la explicarea variabilei dependente (țintă). Cu alte cuvinte, unele variabile nu contribuie la prezicerea variabilei țintă.
matematic, R-pătrat se calculează prin împărțirea suma de pătrate de reziduuri (SSR) la suma totală de pătrate (SStot) și apoi scade-l de la 1. În acest caz, sstot măsoară variația totală. Măsurile SSreg au explicat variația și măsurile SSres variații inexplicabile.,
Ca SSres + SSreg = SStot, R2 = a Explicat variație / Variația Totală
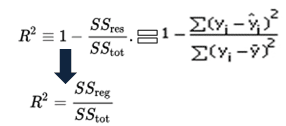
R-squared Ecuație
R-Squared este, de asemenea, numit coeficientul de determinare. Acesta se află între 0% și 100%. O valoare r-pătrat de 100% înseamnă modelul explică toate variația variabilei țintă. Și o valoare de 0% măsoară puterea predictivă zero a modelului. Valoare mai mare R-pătrat, mai bine modelul.
ajustat R-pătrat
măsoară proporția de variație explicată doar de acele variabile independente care ajută cu adevărat la explicarea variabilei dependente., Vă penalizează pentru adăugarea de variabile independente care nu ajută la prezicerea variabilei dependente.
ajustat R-pătrat poate fi calculată matematic în ceea ce privește suma de pătrate. Singura diferență între R-pătrat și ajustat ecuația R-pătrat este gradul de libertate.
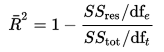
adjusted R-Squared Ecuație
În ecuația de mai sus, dft este de grade de libertate n– 1 de estimare a populației varianța variabilei dependente, și dfe este de grade de libertate n – p – 1 de estimare a populației de bază variație de eroare.,
valoarea ajustată R-pătrat poate fi calculată pe baza valorii R-pătrat, numărul de variabile independente (predictori), dimensiunea totală a eșantionului.

adjusted R-Squared Ecuația 2
Diferența dintre R-pătrat și adjusted R-square
- de Fiecare dată când adăugați o variabilă independentă de la un model, R-squared crește, chiar dacă variabila independentă este nesemnificativă. Nu scade niciodată. În timp ce R-pătrat ajustat crește numai atunci când variabila independentă este semnificativă și afectează variabila dependentă.,
- adjusted r-squared poate fi negativ când r-squared este aproape de zero.
- valoarea ajustată r-pătrat să fie întotdeauna mai mică sau egală cu valoarea r-pătrat.
în tabelul de mai jos, ajustat R-pătrat este maximă atunci când am inclus două variabile. Acesta scade atunci când se adaugă a treia variabilă. În timp ce R-pătrat crește atunci când am inclus a treia variabilă. Înseamnă că a treia variabilă este nesemnificativă pentru model.

R-Squared vs adjusted R-Squared
ajustat R-pătrat ar trebui să fie utilizat pentru a compara modele cu un număr diferit de variabile independente. Ajustat R-pătrat ar trebui să fie utilizat în timp ce selectarea predictori importante (variabile independente) pentru modelul de regresie.
R : calculați R-pătrat și ajustat R-pătrat
Să presupunem că aveți valori variabile dependente reale și prezise. În scriptul de mai jos, am creat un eșantion al acestor valori. În acest exemplu, y se referă la variabila dependentă observată și yhat se referă la variabila dependentă prezisă.,
rezultatul Final: R-pătrat = 0.6410828
să presupunem că aveți trei variabile independente în acest caz.
n = 10
p = 3
adj.r.squared = 1 – (1 – R squared) * ((n – 1)/(n-p-1))
print(adj.r.pătrat)
În acest caz, adjusted r-squared value este 0.4616242 presupunând că avem 3 predictori și 10 observații.