|
wykładniczy wzrost i rozpad
MathBitsNotebook.com Topical Outline | Algebra 2 Outline | MathBits' Teacher Resources Terms of Use Osoba kontaktowa: Donna Roberts |
w algebrze 1 poniższe dwie formuły funkcyjne zostały użyte do łatwego zilustrowania pojęć wzrostu i rozpadu w algebrze 1.stosowane sytuacje., Jeśli ilość rośnie o stały procent w regularnych odstępach czasu, wzór może być przedstawiony przez te funkcje.
|
wzrost wykładniczy:
y = a(1 + r)x |
rozkład wykładniczy:
y = a(1 – r)X |
pamiętaj, że oryginalny wzór wykładniczy to Y = ABX.
zauważysz, że w tych nowych funkcjach wzrostu i rozpadu
wartość b (czynnik wzrostu) została zastąpiona przez (1 + r) lub przez (1 – r).,
„szybkość wzrostu” (r) jest określana jako b = 1 + r.
„szybkość rozpadu” (r) jest określana jako b = 1 – r
r = szybkość wzrostu lub rozpadu (najczęściej reprezentowana jako procent i wyrażona jako dziesiętna)
x = liczba przedziałów czasowych, które przeszły
przykład 1: populacja miasta w 2016 roku została oszacowana na 100%.35 000 osób z roczną stopą wzrostu 2,4%.
a) jaki jest czynnik wzrostu dla miasta?
po roku liczba ludności wynosiła 35 000 + 0,024(35 000).,
przez faktoring mamy 35000 (1 + 0,024) lub 35000 (1,024).
Współczynnik wzrostu wynosi 1,024. (Pamiętaj, że czynnik wzrostu jest większy niż 1.)
|
b) napisz równanie do modelu przyszłego wzrostu.
y = abx = a (1.014)x = 35000 (1.024) x c) użyj równania, aby oszacować liczbę ludności w 2020 r.do najbliższych stu osób. |
 |
![]()
większość naturalnie występujących zjawisk rośnie w sposób ciągły. Na przykład bakterie będą rosły w ciągu 24 godzin, produkując nowe bakterie, które również będą rosły. Bakterie nie czekają do końca 24 godzin, a następnie wszystkie rozmnażają się na raz.
wykładniczy e jest używany przy modelowaniu ciągłego wzrostu, który występuje naturalnie, np. populacje, bakterie, rozpad promieniotwórczy itp., Możesz myśleć o e Jak o uniwersalnej stałej reprezentującej, jak szybko możesz rosnąć za pomocą ciągłego procesu. A piękno e polega na tym, że nie tylko jest on używany do reprezentowania ciągłego wzrostu, ale może również reprezentować wzrost mierzony okresowo w czasie(np. wzrost w przykładzie 1).
w algebrze 2 wykładnicza e będzie używana w sytuacjach ciągłego wzrostu lub rozpadu. Poniższy wzór jest używany do zilustrowania ciągłego wzrostu i rozpadu. Jeśli ilość rośnie w sposób ciągły o stały procent, wzór można przedstawić za pomocą tej funkcji.,
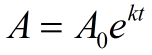
A0 = wartość początkowa (kwota przed pomiarem wzrostu lub rozpadu)
e = wykładnicza e = 2.71828183…,
k = ciągłe tempo wzrostu (zwane również stałą proporcjonalności)
(k > 0, kwota rośnie (rośnie); k < 0, kwota maleje (rozkłada))
T = czas, który minął
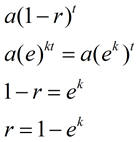 |
jeśli porównamy tę nową formułę do naszej poprzedniej wykładniczej formuły rozpadu (lub formuły wzrostu), możemy zobaczyć, jak ek jest związane z szybkością rozpadu, R (lub wzrostu)., |
(bakterie stale rosną)
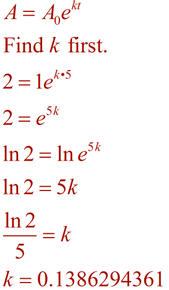 |
teraz Utwórz równanie używając tej wartości k, i rozwiązać problem za pomocą czasu 96 minut.,
|
![]()