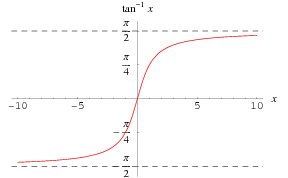
funkcja odwrotnej stycznej 
jest wykreślona powyżej wzdłuż rzeczywistej osi.
co gorsza, notacja 
jest czasami używana dla wartości głównej, a 
jest używana dla funkcji wielowartościowej (Abramowitz and Stegun 1972, s. 80)., Zauważ, że w zapisie 
(powszechnie używanym w Ameryce Północnej i w kalkulatorach kieszonkowych na całym świecie), 
oznacza tangens, a 
funkcja odwrotna, a nie mnożnikowa odwrotność.
główna wartość odwrotnej stycznej jest zaimplementowana jako ArcTan w języku Wolframa. W bibliotece GNU C jest zaimplementowany jako atan (double x).,
odwrotna styczna jest funkcją wielowartościową i dlatego wymaga przecięcia gałęzi w płaszczyźnie złożonej, którą konwencja języka Wolframa umieszcza w
I
., Wynika to z definicji 
as
 |
(1)
|
w języku Wolframa (i w tej pracy) ta definicja cięcia gałęzi określa zakres 
dla rzeczywistego 
jako 
. Należy jednak zachować ostrożność, ponieważ inne definicje cięcia gałęzi mogą dawać różne zakresy (najczęściej 
).,
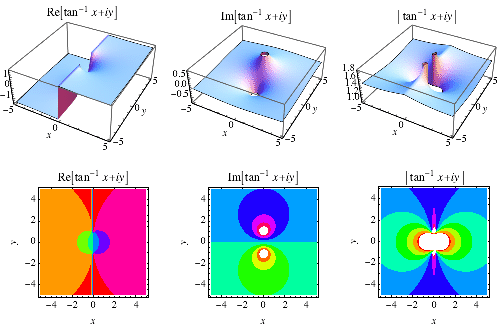
funkcja odwrotnej stycznej
jest wykreślona powyżej w płaszczyźnie złożonej.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
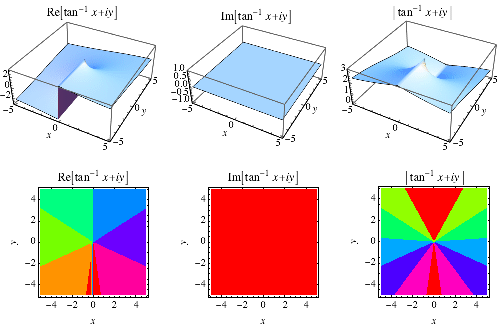
and 
. Plots of 
are illustrated above for real values of 
and 
.,
specjalny rodzaj odwrotnej stycznej, który bierze pod uwagę kwadrant, w którym 
leży i jest zwracany przez polecenie FORTRAN ATAN2(y, x), polecenie biblioteki GNU C atan2(double y, double x) i polecenie języka Wolfram arctan i jest często ograniczony do zakresu 
.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
aby znaleźć
numerycznie można użyć następującego algorytmu przypominającego średnią arytmetyczno-geometryczną.,464e247ac”>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
jest redukowalne iff wszystkie czynniki pierwsze 
występują wśród czynników pierwszych 
dla 
, …, 
. Drugim koniecznym i wystarczającym warunkiem jest to, że największy współczynnik pierwszości 
jest mniejszy niż 
., Równoważnym drugim warunkiem jest twierdzenie, że każda liczba Gregory 
może być jednoznacznie wyrażona jako suma w kategoriach 
s, dla której 
jest liczbą Størmera (Conway and Guy 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway i Guy (1996) podają podobną tabelę pod względem liczb Størmera.,
the finding one of which is a given as a problem by Bailey et al., (2006, s. 225).