R-kwadrat (R2)
mierzy udział zmienności w zmiennej zależnej wyjaśnione przez wszystkie zmienne niezależne w modelu. Zakłada ona, że każda zmienna niezależna w modelu pomaga wyjaśnić zmienność zmiennej zależnej., W rzeczywistości niektóre zmienne niezależne (predyktory) nie pomagają w wyjaśnieniu zmiennej zależnej (docelowej). Innymi słowy, niektóre zmienne nie przyczyniają się do przewidywania zmiennej docelowej.
matematycznie R-kwadrat oblicza się przez podzielenie sumy kwadratów rezydualnych (Ssre) przez sumę kwadratów całkowitych (Sstot), a następnie odjęcie jej od 1. W tym przypadku sstot mierzy całkowitą zmienność. Środki SSreg wyjaśnione zmiany i środki SSres niewyjaśnione zmiany.,
As SSres + SSreg = SStot, R2 = Explained variation / Total Variation
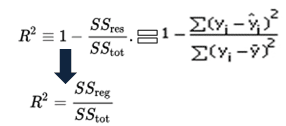
R-kwadrat równanie
R-kwadrat jest również nazywany współczynnik determinacji. Leży pomiędzy 0% a 100%. Wartość R-kwadratowa 100% oznacza, że model wyjaśnia wszystkie zmiany zmiennej docelowej. A wartość 0% mierzy zerową moc predykcyjną modelu. Wyższa wartość R-kwadrat, lepszy model.
skorygowany R-kwadrat
mierzy proporcję zmienności wyjaśnioną tylko tymi niezależnymi zmiennymi, które naprawdę pomagają w wyjaśnieniu zmiennej zależnej., Karze cię za dodanie zmiennej niezależnej, która nie pomaga w przewidywaniu zmiennej zależnej.
skorygowany R-kwadrat można obliczyć matematycznie jako sumę kwadratów. Jedyną różnicą między R-kwadratem a skorygowanym r-kwadratem jest stopień swobody.
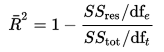
skorygowane równanie R-kwadratowe
w powyższym równaniu dft to stopnie swobody n– 1 oszacowania wariancji populacji zmiennej zależnej, a dfe to stopnie swobody n – p – 1 oszacowania wariancji błędu populacji podstawowej.,
skorygowaną wartość R-kwadrat można obliczyć na podstawie wartości R-kwadrat, liczby zmiennych niezależnych( predyktorów), całkowitej wielkości próby.

skorygowane równanie R-kwadrat 2
różnica między R-kwadratem a skorygowanym R-kwadratem
- za każdym razem, gdy dodajesz zmienną niezależną do modelu, R-kwadrat wzrasta, nawet jeśli zmienna niezależna jest nieistotna. Nigdy się nie zmniejsza. Natomiast skorygowany R-kwadrat zwiększa się tylko wtedy, gdy zmienna niezależna jest znacząca i wpływa na zmienną zależną.,
- skorygowany R-kwadrat może być ujemny, gdy R-kwadrat jest bliski zeru.
- skorygowana wartość R-kwadrat zawsze jest mniejsza lub równa wartości R-kwadrat.
w poniższej tabeli skorygowany r-kwadrat jest maksymalny, gdy uwzględniliśmy dwie zmienne. Zmniejsza się po dodaniu trzeciej zmiennej. Natomiast R-kwadrat zwiększa się, gdy włączyliśmy trzecią zmienną. Oznacza to, że trzecia zmienna jest nieistotna dla modelu.

R-kwadrat vs.skorygowany R-kwadrat
skorygowany kwadrat R powinien być używany do porównywania modeli z różnymi liczbami zmiennych niezależnych. Skorygowany R-kwadrat powinien być stosowany przy wyborze ważnych predyktorów (zmiennych niezależnych) dla modelu regresji.
R : Oblicz R-kwadrat i skoryguj R-kwadrat
Załóżmy, że masz rzeczywiste i przewidywane wartości zmiennych zależnych. W poniższym skrypcie stworzyliśmy próbkę tych wartości. W tym przykładzie y odnosi się do obserwowanej zmiennej zależnej, a yhat odnosi się do przewidywanej zmiennej zależnej.,
wynik końcowy : R-kwadrat = 0.6410828
Załóżmy, że w tym przypadku masz trzy niezależne zmienne.
n = 10
p = 3
ADJ.r.squared = 1 – (1 – R.squared) * ((n – 1)/(n-p-1))
print(adj.R.squared)
w tym przypadku skorygowana wartość R-squared wynosi 0.4616242 zakładając, że mamy 3 predyktory i 10 obserwacji.