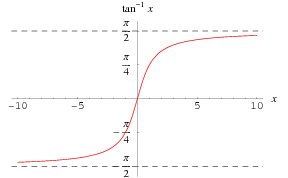
de inverse rangent functie
wordt boven langs de reële as uitgezet.
erger nog, de notatie 
wordt soms gebruikt voor de hoofdwaarde, waarbij 
wordt gebruikt voor de functie met meerdere waarden (Abramowitz and Stegun 1972, p. 80)., Merk op dat in de notatie 
(algemeen gebruikt in Noord-Amerika en in zakrekenmachines wereldwijd), 
de tangens aangeeft en 
de inverse functie, niet de multiplicatieve inverse.
de hoofdwaarde van de inverse raaklijn wordt geïmplementeerd als ArcTan in de Wolframtaal. In de GNU C-bibliotheek wordt het geà mplementeerd als atan (double x).,
de inverse raaklijn is een functie met meerdere waarden en vereist daarom een vertakking in het complexe vlak, dat de wolframtaal op 
en 
plaatst., Dit volgt uit de definitie van 
als
 |
(1)
|
In de Wolfram Taal (en in dit werk), deze tak gesneden definitie hiermee wordt het bereik bepaald van 
voor de echte 
als 
. Voorzichtigheid is echter geboden, omdat andere branch cut definities verschillende bereiken kunnen geven (meestal 
).,
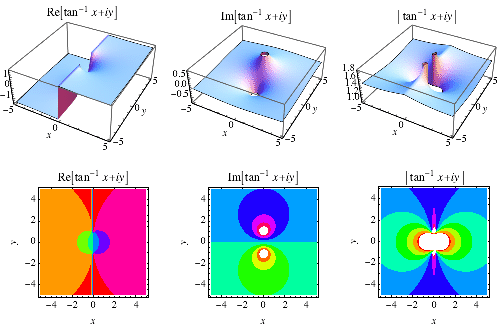
de inverse rangent functie 
wordt hierboven in het complexe vlak uitgezet.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
and 
. Plots of 
are illustrated above for real values of 
and 
.,
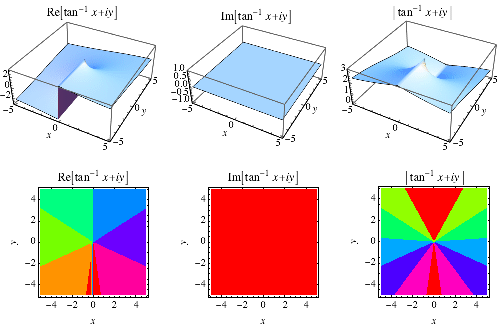
een speciaal soort inverse raaklijn die rekening houdt met het kwadrant waarin 
ligt en wordt geretourneerd door het FORTRAN Commando ATAN2(y, x), het GNU C library Commando atan2(double y, double x), en het Wolfram Language Commando ArcTan, en is vaak beperkt naar het bereik 
.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
om 
numeriek te vinden, kan het volgende rekenkundig-geometrisch gemiddelde-achtige algoritme worden gebruikt.,464e247ac”>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
is reduceerbaar iff alle priemfactoren van 
komen voor onder de priemfactoren van 
voor 
…, 
. Een tweede noodzakelijke en voldoende voorwaarde is dat de grootste priemfactor van 
kleiner is dan 
., Equivalent aan de tweede voorwaarde is de stelling dat elk Gregory-getal 
uniek kan worden uitgedrukt als een Som in termen van 
s waarvoor 
een Størmer-getal is (Conway and Guy 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway and Guy (1996) geven een vergelijkbare tabel in termen van Størmer nummers.,
the finding one of which is a given as a problem by Bailey et al., (2006, blz. 225).