|
Exponentiële Groei en Verval
MathBitsNotebook.com Actueel Overzicht | Algebra 2 Overzicht | MathBits’ Teacher Resources Voorwaarden van Gebruik de Contact Persoon: Donna Roberts |
In de Algebra 1, de volgende twee functies formules werden gebruikt om eenvoudig illustratie van de concepten van groei en verval in toegepaste situaties., Als een hoeveelheid met een vast percentage groeit met regelmatige tussenpozen, kan het patroon worden afgebeeld door deze functies.
|
Exponentiële Groei:
y = a(1 + r)x |
Exponentieel Verval:
y = a(1 – r)x |
Vergeet niet dat de oorspronkelijke exponentiële formule is y = abx.
U zult merken dat in deze nieuwe groei-en vervalfuncties,
De B-waarde (groeifactor) is vervangen door (1 + r) of door (1 – r).,
het groeipercentage (R) wordt bepaald als b = 1 + r.
Het vervalpercentage (r) wordt bepaald als b = 1 – r
r = groeipercentage (meestal weergegeven als een percentage en uitgedrukt als een decimaal)
x = aantal tijdsintervallen die
zijn gepasseerd Voorbeeld 1: de populatie van geboortestad is 2016 werd geschat op 35.000 mensen met een jaarlijks stijgingspercentage van 2,4%.
a) Wat is de groeifactor voor geboortestad?na een jaar zou de bevolking 35.000 + 0,024(35000) zijn.,
door factoring hebben we 35000(1 + 0,024) of 35000(1,024).de groeifactor is 1,024. (Onthoud dat de groeifactor groter is dan 1.)
|
b) Schrijf een vergelijking om toekomstige groei te modelleren.
y = abx = a(1,014)x = 35000 (1,024)x c) Gebruik de vergelijking om de populatie in 2020 te schatten tot op de dichtstbijzijnde honderd mensen. |
 |
![]()
de meeste van nature voorkomende verschijnselen groeien voortdurend. Bacteriën zullen bijvoorbeeld gedurende een periode van 24 uur blijven groeien, waardoor nieuwe bacteriën ontstaan die ook zullen groeien. De bacteriën wachten niet tot het einde van de 24 uur, en planten zich dan allemaal tegelijk voort. de exponentiële e wordt gebruikt bij het modelleren van continue groei die van nature voorkomt, zoals populaties, bacteriën, radioactief verval, enz., Je kunt denken aan e als een universele constante die aangeeft hoe snel je zou kunnen groeien met behulp van een continu proces. En, het mooie van e is dat het niet alleen wordt gebruikt om continue groei te vertegenwoordigen, maar het kan ook de groei periodiek gemeten in de tijd vertegenwoordigen (zoals de groei in Voorbeeld 1).
in Algebra 2 wordt de exponentiële e gebruikt in situaties van continue groei of verval. De volgende formule wordt gebruikt om continue groei en verval te illustreren. Als een hoeveelheid continu groeit met een vast percentage, kan het patroon worden afgebeeld door deze functie.,
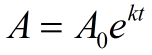
A0 = beginwaarde (bedrag vóór het meten van groei of verval)
e = exponentieel e = 2.71828183…,
k = continue groei (ook wel constante van evenredigheid)
k > 0, het bedrag is het vergroten van de (groeiende); k < 0, wordt de hoeveelheid wind (rottend))
t = de tijd die verstreken
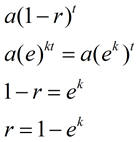 |
Als we vergelijken met deze nieuwe formule voor onze vorige exponentieel verval formule (of groei formule), we kunnen zien hoe ek is gerelateerd aan de snelheid van verval, r, (of groei)., |
(bacteriën groeien continu)
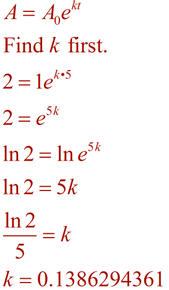 |
Maak nu de vergelijking met deze K-waarde en los het probleem op met behulp van de tijd van 96 minuten.,
|
![]()