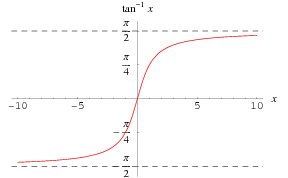
La tangente inversa funzione 
è tracciata sopra lungo l’asse reale.
Peggio ancora, la notazione 
viene talvolta utilizzata per il valore principale, con 
utilizzata per la funzione multivalore (Abramowitz e Stegun 1972, p. 80)., Si noti che nella notazione 
(comunemente usata in Nord America e nelle calcolatrici tascabili di tutto il mondo), 
indica la tangente e 
la funzione inversa, non l’inverso moltiplicativo.
Il valore principale della tangente inversa è implementato come ArcTan nel linguaggio Wolfram. Nella libreria GNU C, è implementato come atan (double x).,
La tangente inversa è una funzione multivalore e quindi richiede un taglio di ramo nel piano complesso, che la convenzione del linguaggio Wolfram pone a
e
., Questo segue dalla definizione di 
come
 |
(1)
|
Nel Wolfram Language (e in questo lavoro), questo ramo tagliato definizione determina l’intervallo di 
reale 
come 
. Occorre prestare attenzione, tuttavia, poiché altre definizioni di taglio di ramo possono fornire intervalli diversi (più comunemente, 
).,
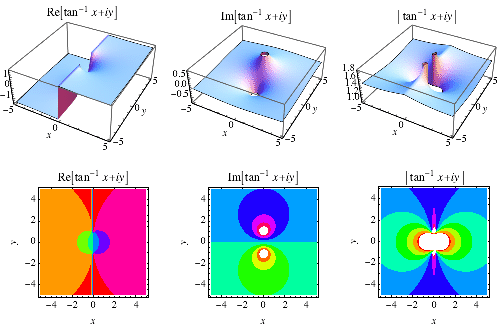
La funzione tangente inversa
è tracciata sopra nel piano complesso.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
and 
. Plots of 
are illustrated above for real values of 
and 
.,
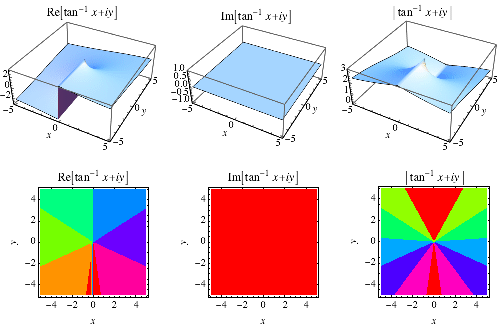
Un particolare tipo di tangente inversa, che tiene conto del quadrante in cui 
si trova e viene restituito da FORTRAN comando ATAN2(y, x), la libreria GNU C comando atan2(double y, double x), e la Wolfram Language comando ArcTan e spesso limitati all’intervallo 
.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
Per trovare
numericamente, è possibile utilizzare il seguente algoritmo di media aritmetica-geometrica.,464e247ac”>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
è riducibile se tutti i fattori primi di
si verificano tra i fattori primi di
per
,…, 
. Una seconda condizione necessaria e sufficiente è che il più grande fattore primo di 
è inferiore a
., Equivalente alla seconda condizione è l’affermazione che ogni numero di Gregory
può essere espresso in modo univoco come somma in termini di
per cui
è un numero di Størmer (Conway e Guy 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway e Guy (1996) danno una tabella simile in termini di numeri di Størmer.,
the finding one of which is a given as a problem by Bailey et al., (2006, pag. 225).