|
Esponenziale di Crescita e di Decadimento
MathBitsNotebook.com Attualità Contorno | Algebra 2 Schema | MathBits’ Risorse per l’Insegnante Termini di Utilizzo, Persona di Contatto: Donna Roberts |
In Algebra 1, le due funzioni seguenti formule sono state usate per illustrare i concetti di crescita e di decadimento applicata situazioni., Se una quantità cresce di una percentuale fissa a intervalli regolari, il modello può essere rappresentato da queste funzioni.
|
Crescita Esponenziale:
y = a(1 + r)x |
Decadimento Esponenziale:
y = a(1 – r)x |
Ricordiamo che l’originale esponenziale formula y = abx.
Noterai che in queste nuove funzioni di crescita e decadimento,
il valore b (fattore di crescita) è stato sostituito da (1 + r) o da (1 – r).,
La crescita “tasso” (r) è determinato come b = 1 + r.
Il decadimento “tasso” (r) è determinato come b = 1 – r
r = crescita o il tasso di decadimento (più spesso rappresentata come una percentuale, espressa in decimali)
x = numero di intervalli di tempo che sono passati
Esempio 1: La popolazione della Città è il 2016 è stato stimato a 35.000 persone, con un tasso annuale di aumento del 2,4%.
a) Qual è il fattore di crescita per la città natale?
Dopo un anno la popolazione sarebbe 35.000 + 0.024(35000).,
Di factoring, abbiamo 35000(1 + 0.024) o 35000(1.024).
Il fattore di crescita è 1.024. (Ricordate che il fattore di crescita è maggiore di 1.)
|
b) Scrivi un’equazione per modellare la crescita futura.
y = abx = a(1.014)x = 35000(1.024)x c) Usa l’equazione per stimare la popolazione nel 2020 alle centinaia di persone più vicine. |
 |
![]()
la Maggior parte dei naturali fenomeni di crescere continuamente. Ad esempio, i batteri continueranno a crescere per un periodo di 24 ore, producendo nuovi batteri che cresceranno anche. I batteri non aspettano fino alla fine delle 24 ore e poi si riproducono tutti contemporaneamente.
L’esponenziale e viene utilizzato quando si modella la crescita continua che si verifica naturalmente come popolazioni, batteri, decadimento radioattivo, ecc., Puoi pensare a e come una costante universale che rappresenta la velocità con cui potresti crescere usando un processo continuo. E, la bellezza di e è che non solo è usato per rappresentare la crescita continua, ma può anche rappresentare la crescita misurata periodicamente nel tempo (come la crescita nell’esempio 1).
In Algebra 2, l’esponenziale e verrà utilizzato in situazioni di crescita continua o decadimento. La seguente formula viene utilizzata per illustrare la crescita e il decadimento continui. Se una quantità cresce continuamente di una percentuale fissa, il modello può essere rappresentato da questa funzione.,
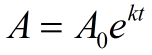
A0 = valore iniziale (importo prima di misurare crescita o decadimento)
e = esponenziale e = 2.71828183…,
k = continuo del tasso di crescita (anche chiamato costante di proporzionalità)
(k > 0, la quantità è in aumento (in crescita); k < 0, la quantità è in diminuzione (decadente))
t = tempo che è passato
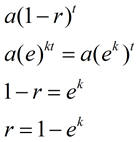 |
Se confrontiamo questa nuova formula del nostro precedente decadimento esponenziale formula (o formula di crescita), possiamo vedere come ek è legato al tasso di decadimento, r, (o di crescita)., |
(i batteri crescono continuamente)
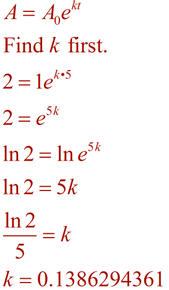 |
Ora, formare l’equazione utilizzando questo valore k, e risolvi il problema usando il tempo di 96 minuti.,
|
![]()