Differenza tra rettificato R-quadrato e R-quadrato

R-squared (R2)
Misura la proporzione della variazione nella variabile dipendente spiegata da tutte le variabili indipendenti nel modello. Presuppone che ogni variabile indipendente nel modello aiuti a spiegare la variazione nella variabile dipendente., In realtà, alcune variabili indipendenti (predittori) non aiutano a spiegare la variabile dipendente (target). In altre parole, alcune variabili non contribuiscono a predire la variabile di destinazione.
Matematicamente, R-squared è calcolato dividendo somma dei quadrati di residui (SSres) per somma totale dei quadrati (SStot) e quindi sottrarlo da 1. In questo caso, SStot misura la variazione totale. Misure SSreg spiegato variazione e misure SSres variazione inspiegabile.,
As SSres + SSreg = SStot, R2 = Explained variation / Total Variation

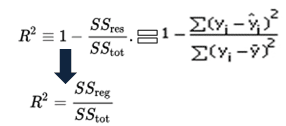
R-squared Equation

R-Squared è anche chiamato coefficiente di determinazione. Si trova tra 0% e 100%. Un valore r-quadrato del 100% indica che il modello spiega tutte le variazioni della variabile target. E un valore di 0% misura zero potenza predittiva del modello. Valore R-quadrato più alto, migliore il modello.
Aggiustato R-Quadrato
Misura la proporzione di variazione spiegata solo da quelle variabili indipendenti che aiutano davvero a spiegare la variabile dipendente., Ti penalizza per l’aggiunta di variabili indipendenti che non aiutano a prevedere la variabile dipendente.
Rettificato R-quadrato può essere calcolato matematicamente in termini di somma dei quadrati. L’unica differenza tra R-quadrato e l’equazione R-quadrato regolata è il grado di libertà.

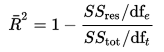
Equazione R-quadrato aggiustata

Nell’equazione precedente, dft è il grado di libertà n– 1 della stima della varianza di popolazione della variabile dipendente e dfe è il grado di libertà n – p – 1 della stima della varianza di errore di popolazione sottostante.,
Il valore R-quadrato regolato può essere calcolato in base al valore di r-quadrato, al numero di variabili indipendenti (predittori), alla dimensione totale del campione.

Equazione R-quadrato regolata 2

Differenza tra R-quadrato e R-quadrato regolato

1. Ogni volta che si aggiunge una variabile indipendente a un modello, l’R-quadrato aumenta, anche se la variabile indipendente è insignificante. Non declina mai. Considerando che l’R-quadrato aggiustato aumenta solo quando la variabile indipendente è significativa e influenza la variabile dipendente.,

Nella tabella seguente, r-quadrato regolato è massimo quando abbiamo incluso due variabili. Declina quando viene aggiunta la terza variabile. Considerando che r-squared aumenta quando abbiamo incluso la terza variabile. Significa che la terza variabile è insignificante per il modello.



R-Quadrato vs R-quadrato regolato

2. r-quadrato regolato può essere negativo quando r-quadrato è vicino a zero.
3. Il valore r-quadrato aggiustato è sempre minore o uguale al valore r-quadrato.

R-square regolato dovrebbe essere usato per confrontare modelli con diversi numeri di variabili indipendenti. R-square regolato dovrebbe essere usato durante la selezione di importanti predittori (variabili indipendenti) per il modello di regressione.

R : Calcola R-Quadrato e R-quadrato regolato
Supponiamo di avere valori variabili dipendenti effettivi e previsti. Nello script qui sotto, abbiamo creato un esempio di questi valori. In questo esempio, y si riferisce alla variabile dipendente osservata e yhat si riferisce alla variabile dipendente prevista.,
Risultato finale : R-Squared = 0.6410828
Supponiamo di avere tre variabili indipendenti in questo caso.

n = 10
p = 3
adj.r.squared = 1 – (1 – R. squared) * ((n – 1)/(n-p-1))
print(adj.r.squared)

In questo caso, il valore r-squared regolato è 0.4616242 supponendo che abbiamo 3 predittori e 10 osservazioni.

Python: Calcola R-quadrato e R-quadrato regolati