Origami Cube (Magyar)

Origami Cube

Contents of this Page What is the Origami Cube? Folding the OrigamiCube Some Mathematics Origami Cubeon the Internet .

To the Main Page “Mathematische Basteleien”

What is the Origami Cube?,

…	az origami kocka egy kocka, amelyet egy papír négyzetből lehet összehajtani. egy másik név a vízbomba.

Folding theOrigami Cubetop
1

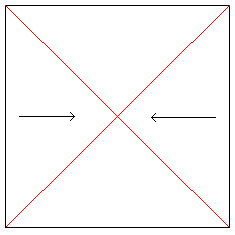hajtson egy négyzet alakú papírlapot az átlón és bontsa ki. helyezze a papírt mindkét nyílra együtt. helyezze a háromszögeket a tetejére, alul pedig a tetejéreegymásról.,

2

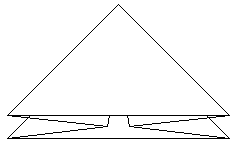The result is a flier triangle, which is known from theswallow or the pigeon.

3

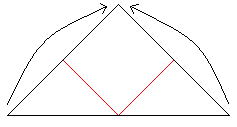Fold upward on the red line on the right and on the left.,

4

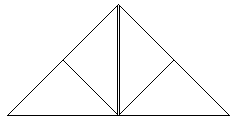Then it must look like this.

5

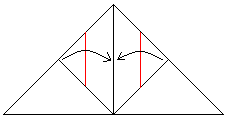Fold on the red lines.,

6

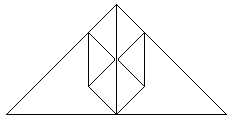Then it must look like this.

7

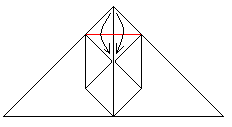Fold the two little triangles on the red lines downward.,

8

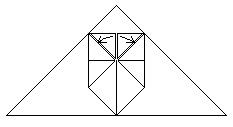Put the last made triangles in the two pockets on theright and on the left. This is a little bit fiddly.

9

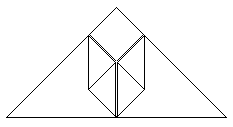Then it must look like this.,

10

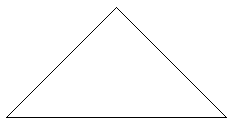Turn the whole triangle and repeat the steps 3,4,5,6,7,8,9.

11

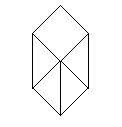Then it must look like this.,

12

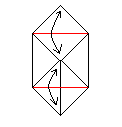Fold and unfold on the red lines.

13

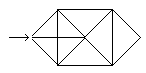Take the folded cube in hand and blow into the hole atthe top. Unfold the cube by this.,

14

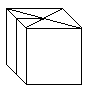finished

Some Mathematics top

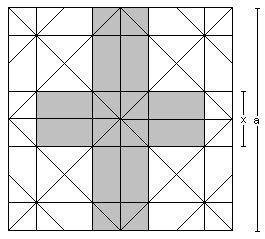If you take the cube apart, you get a nice pattern, whichis made by the folds. You find the formulas: ………,

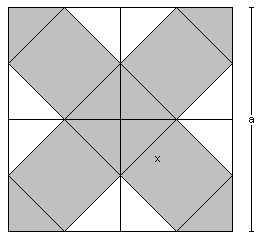a bal oldalon látható a kocka legnagyobb hálója, amelyegy négyzetet alkot. megtalálja a képleteket: Ez a kocka sokkal nagyobb, mint a hajtogatott kocka.,

Ha az egész tér egy kocka, van képlet:

Ez a legnagyobb kocka, elméletileg.

Lásd még: könyv (5), oldal 63f. és oldal 71ff. “Dereingewickelte Würfel”.

OrigamiCube on the Internet

Englisch

Dr. Stephen O ‘ Hanlon(Ring of Origami Art)
WaterBomb ( .,pdf file)

Gerwin Sturm (Origami mindenkinek)
Waterbomb

Puzzle Playground (Puzzle_com)
Squareto Cube

Wikipedia
Waterballoon

angol

Jennifer ‘ sPuzzle
3 csíkból álló kocka fonása

Umwelthaus Pinneberg E. V.,
Wasserbombeaus papír

a Wikipédia
víz-bomba(játék)

zzzebra
víz bomba

Hivatkozások felső
(1) Joachim Schönherr, Mi hajtás, összecsukható, Leipzig1990
(2) Therese Mielhaht: Origami szórakoztató papír hajtogatás,Köln, 1990
(3) Kunihiko Kasahara Origami figuratív, valamint a geometriai,München, 2000
(4) Kunihiko Kasahara Origami határok nélkül, München2001
(5) Martin Gardner: Matematikai varázslás, Berlin/frankfurtammain/Bécs 1988