div>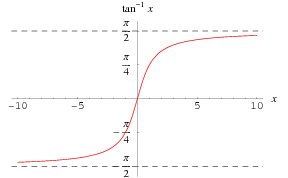
az inverz érintő függvény 
a valós tengely mentén van ábrázolva.
ami még rosszabb, a
jelölést néha a főértékre használják, a
többértékű funkcióhoz (Abramowitz and Stegun 1972, 80. o.)., Vegye figyelembe, hogy a 
(Észak-Amerikában és a zsebszámítógépekben világszerte általánosan használt) jelölésben a 
az érintőt jelöli, és a 
az inverz függvényt, nem a multiplikatív inverzt.
az inverz tangens fő értékét Arctanként valósítják meg a Wolfram nyelvben. A GNU C könyvtárban atan(double x) néven kerül végrehajtásra.,
az inverz tangens többértékű függvény, ezért a komplex síkban elágazást igényel, amelyet a Wolfram nyelv konvenciója a 
és 
., Ez a 
as
 |
(1)
div> |
a Wolfram nyelven (és ebben a munkában) ez az ágvágási definíció határozza meg a 
tartományt a real 
as 
. Ügyelni kell azonban, mivel más ágvágási definíciók különböző tartományokat adhatnak (leggyakrabban 
).,
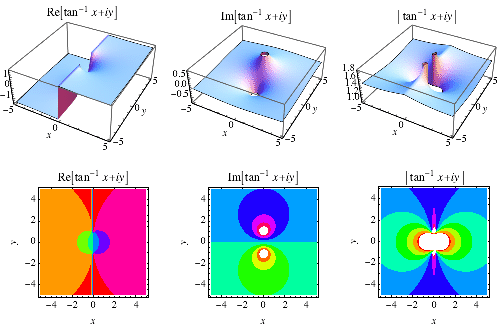
az inverz érintő függvény 
a komplex síkban van ábrázolva.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
and 
. Plots of 
are illustrated above for real values of 
and 
.,
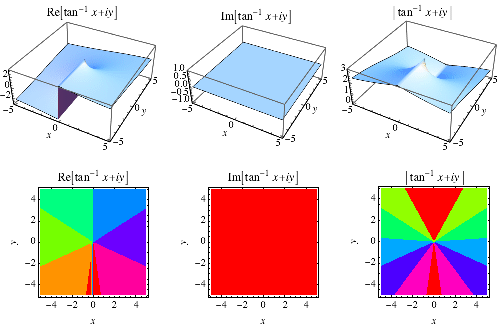
egy speciális inverz tangens, amely figyelembe veszi azt a kvadránsot, amelyben a 
az ATAN2(y, x) FORTRAN parancs, a GNU C könyvtár parancs atan2(double y, double x) és a Wolfram nyelv parancs arctan, és gyakran csak a 
tartományra korlátozódik.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
a 
numerikusan a következő aritmetikai-geometriai átlagszerű algoritmus használható.,464e247ac”>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
a
összes prímtényezője
…, 
. A második szükséges és elégséges feltétel, hogy a 
legnagyobb prímtényezője kisebb, mint a
., A második feltételnek megfelelő az a kijelentés, hogy minden Gregory-szám 
egyedileg kifejezhető 
s összegben, amelyre 
egy Størmer-szám (Conway and Guy 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway és Guy (1996) hasonló táblázatot adnak a Størmer számok tekintetében.,
the finding one of which is a given as a problem by Bailey et al., (2006, 225. o.).