Exponenciális Növekedés, valamint a Hanyatlás – MathBitsNotebook(A2

Exponenciális Növekedés, valamint a Bomlás MathBitsNotebook.com Lokális Vázlat | Algebra 2 Vázlat | MathBits’ Tanár Források Felhasználási feltételek Kapcsolattartó Személy: Donna Roberts

Algebra 1, a következő két funkció formulákat használtak, hogy könnyen illusztrálására, a fogalmak, a növekedés, a bomlás az alkalmazott helyzetekben., Ha egy mennyiség rendszeres időközönként rögzített százalékkal növekszik, akkor a mintát ezek a funkciók ábrázolhatják.

Exponenciális Növekedés: y = (1 + r)x

Exponenciális Bomlás: y = a(1 – r)x

ne feledje, hogy az eredeti exponenciális egyenletet y = abx.
észre fogod venni, hogy ezekben az új növekedési és bomlási funkciókban
A b értéket (növekedési faktor) vagy (1 + r) vagy (1 – r) váltotta fel.,
a növekedési “sebesség” (r) meghatározása: b = 1 + r.
a bomlási “sebesség” (r) meghatározása: b = 1 – r

a = kezdeti érték (a növekedés vagy bomlás mérése előtti összeg)
r = növekedési vagy bomlási sebesség (leggyakrabban százalékban kifejezve, decimális értékként kifejezve)
x = a

1.példa: a szülőváros népessége 2016-ra becsülték legyen 35,000 emberek éves növekedési üteme 2.4%.
A) mi a szülőváros növekedési tényezője?
egy év elteltével a lakosság 35 000 + 0,024(35000) lenne.,
faktorálással 35000(1 + 0.024) vagy 35000(1.024) van.
a növekedési faktor 1,024. (Ne feledje, hogy a növekedési faktor nagyobb, mint 1.)

B) írjon egy egyenletet a jövőbeli növekedés modellezéséhez. y = abx = a (1.014)x = 35000 (1.024)x c) használja az egyenletet a népesség becsléséhez 2020-ban a legközelebbi száz emberhez. y = 35000(1,024)4 ≈ 38,482.,91 ≈ 38,500

a legtöbb természetben előforduló jelenség folyamatosan növekszik. Például a baktériumok 24 órán keresztül tovább fognak növekedni, új baktériumokat termelnek, amelyek szintén növekedni fognak. A baktériumok nem várnak a 24 óra végéig, majd egyszerre reprodukálódnak.
Az exponenciális e-t a természetes módon előforduló folyamatos növekedés modellezésekor használják, például populációk, baktériumok, radioaktív bomlás stb., Úgy gondolhat az E-re, mint egy univerzális állandóra, amely azt mutatja, hogy milyen gyorsan tud növekedni egy folyamatos folyamat segítségével. Az e szépsége az, hogy nem csak a folyamatos növekedés ábrázolására használják, hanem az idő múlásával időszakosan mért növekedést is képviselheti (például az 1.példa növekedését).

a 2. algebrában az exponenciális e-t folyamatos növekedés vagy bomlás esetén használják. A következő képletet használjuk a folyamatos növekedés és bomlás szemléltetésére. Ha egy mennyiség folyamatosan növekszik egy rögzített százalékkal, akkor a minta ábrázolható ezzel a funkcióval.,

folyamatos exponenciális növekedés vagy bomlás

a = végződő érték(a növekedés vagy bomlás utáni összeg)
A0 = kezdeti érték(a növekedés vagy bomlás mérése előtt)
e = exponenciális e = 2.71828183…,
k = folyamatos növekedési ráta (más néven állandó az arányosság)
(k > 0, a mennyiség növelése (növekvő); k < 0, az összeg csökken (rothadó))
t = idő telt el,

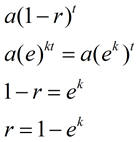Ha összehasonlítjuk ezt az új képlet, hogy a korábbi exponenciális bomlás képlet (vagy növekedés képlet), láthatjuk, hogy az ek kapcsolódik az arány a bomlás, r, (vagy növekedés).,

példa: az asztalon növekvő baktériumtörzs 5 percenként megduplázódik. Feltételezve, hogy csak egy baktériummal kezdődik, hány baktérium lehet jelen a 96 perc végén?
(a baktériumok folyamatosan növekednek)

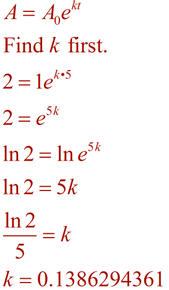most képezzük az egyenletet ezzel a K értékkel, a problémát 96 perc alatt oldja meg.,