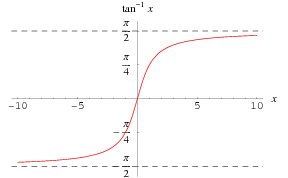
l’inverse de La fonction tangente 
est tracée ci-dessus le long de l’axe réel.
pire encore, la notation 
est parfois utilisée pour la valeur principale, avec 
étant utilisée pour la fonction multivaluée (Abramowitz et Stegun 1972, p. 80)., Notez que dans la notation
(couramment utilisée en Amérique du Nord et dans les calculatrices de poche dans le monde entier),
désigne la tangente et
la fonction inverse, pas l’inverse multiplicatif.
la valeur principale de la tangente inverse est implémentée comme ArcTan dans le langage Wolfram. Dans la bibliothèque GNU C, il est implémenté comme atan (double x).,
la tangente inverse est une fonction multivaluée et nécessite donc une coupe de branche dans le plan complexe, que la convention du Wolfram Language place à
Et
., Cela découle de la définition de 
que
 |
(1)
|
Dans le Wolfram Langue (et dans ce travail), cette branche coupée définition détermine la plage de 
réel 
. Il faut cependant faire attention, car d’autres définitions de coupe de branche peuvent donner des plages différentes (le plus souvent, 
).,
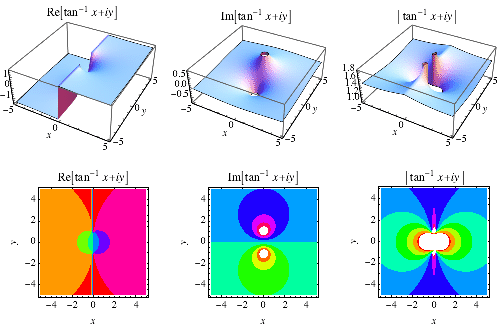
l’inverse de La fonction tangente 
est tracée ci-dessus dans le plan complexe.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
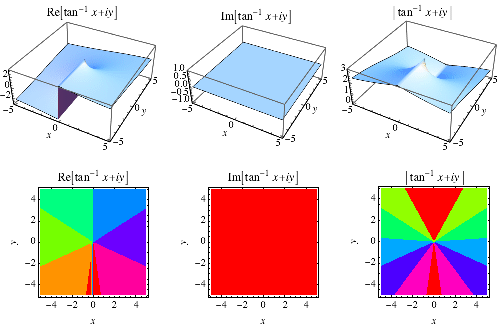
and 
. Plots of 
are illustrated above for real values of 
and 
.,
un type particulier de tangente inverse qui prend en compte le quadrant dans lequel 
se trouve et est retourné par la commande FORTRAN ATAN2(y, x), la commande GNU C library atan2(double y, double x), et le Wolfram Language commande arctan, et est souvent limité à la plage 
.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
pour trouver
numériquement, l’algorithme arithmétique-géométrique suivant peut être utilisé.,464e247ac »>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
est réductible iff tous les facteurs premiers de 
se produire parmi les facteurs premiers de 
par 
, …, 
. Une deuxième condition nécessaire et suffisante est que le plus grand facteur premier de 
a moins de 
., L’équivalent de la deuxième condition est l’affirmation que chaque nombre de Gregory 
peut être exprimé de manière unique comme une somme en termes de 
s pour lequel 
est un nombre de Størmer (Conway et Guy 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway et Guy (1996) donnent un tableau similaire en termes de nombres de Størmer.,
the finding one of which is a given as a problem by Bailey et al., (2006, p. 225).