|
Exponentielle de Croissance et de Décroissance
MathBitsNotebook.com Actualité Contour | Algèbre 2 Plan | MathBits’ Ressources pour les Enseignants, Conditions d’Utilisation: Personne à Contacter: Donna Roberts |
En Algèbre 1, les deux formules ont été utilisées pour illustrer facilement les concepts de croissance et de décroissance dans des situations concrètes., Si une quantité augmente d’un pourcentage fixe à intervalles réguliers, le motif peut être représenté par ces fonctions.
|
Croissance Exponentielle:
y = a(1 + r)x |
Décroissance Exponentielle:
y = a(1 – r)x |
Rappelez-vous que l’original exponentielle de la formule y = abx.
vous remarquerez que dans ces nouvelles fonctions de croissance et de décroissance,
la valeur b (facteur de croissance) a été remplacée par (1 + r) ou par (1 – r).,
le « taux » de croissance (r) est déterminé comme b = 1 + R.
le « taux » de décroissance (r) est déterminé comme b = 1 – r
R = taux de croissance ou de décroissance (le plus souvent représenté en pourcentage et exprimé en décimal)
x = nombre soit 35 000 personnes avec un taux d’augmentation annuel de 2,4%.
A) Quel est le facteur de croissance pour la ville natale?
Après un an, la population serait de 35 000 + 0,024(35 000).,
Par affacturage, nous avons 35000(1 + 0.024) ou 35000(1.024).
Le facteur de croissance est de 1,024. (Rappelez-vous que le facteur de croissance est supérieur à 1.)
|
b) Écris une équation du modèle de croissance future.
y = abx = a(1.014)x = 35000(1.024)x c) utilisez l’équation pour estimer la population en 2020 à la centaine de personnes la plus proche. |
 |
![]()
la Plupart des phénomènes naturels de croître continuellement. Par exemple, les bactéries continueront à se développer sur une période de 24 heures, produisant de nouvelles bactéries qui se développeront également. Les bactéries n’attendent pas la fin des 24 heures, puis se reproduisent toutes à la fois.
l’exponentielle e est utilisée lors de la modélisation de la croissance continue qui se produit naturellement comme les populations, les bactéries, la désintégration radioactive, etc., Vous pouvez penser à e comme une constante universelle représentant la vitesse à laquelle vous pourriez éventuellement croître en utilisant un processus continu. Et, la beauté de e est que non seulement il est utilisé pour représenter la croissance continue, mais il peut également représenter la croissance mesurée périodiquement à travers le temps (comme la croissance dans L’exemple 1).
en algèbre 2, l’exponentielle e sera utilisée dans des situations de croissance ou de décroissance continue. La formule suivante est utilisée pour illustrer la croissance et la décroissance continues. Si une quantité croît continuellement d’un pourcentage fixe, le motif peut être représenté par cette fonction.,
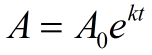
A0 = valeur initiale (montant avant de faire la mesure de la croissance ou de décroissance)
e = exponentielle e = 2.71828183…,
K = taux de croissance continu (également appelé constante de proportionnalité)
(k > 0, le montant augmente (croissant); k < 0, le montant diminue (décroissant))
T = temps écoulé
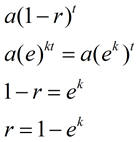 |
si nous comparons cette nouvelle formule à notre précédente formule de décroissance exponentielle (ou formule de croissance), nous pouvons voir comment ek est lié au taux de décroissance, R, (ou croissance)., |
(Les bactéries se développent continuellement)
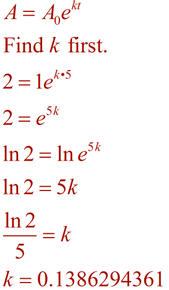 |
maintenant, formez l’équation en utilisant cette valeur k, et résoudre le problème en utilisant le temps de 96 minutes.,
|
![]()