R-squared (R2)
Il mesure la proportion de la variation de votre variable dépendante expliquée par toutes vos variables indépendantes dans le modèle. Il suppose que chaque variable indépendante du modèle aide à expliquer la variation de la variable dépendante., En réalité, certaines variables indépendantes (prédicteurs) n’aident pas à expliquer la variable dépendante (cible). En d’autres termes, certaines variables ne contribuent pas à prédire la variable cible.
mathématiquement, R-squared est calculé en divisant la somme des carrés des résidus (SSres) par la somme totale des carrés (SStot), puis en la soustrayant de 1. Dans ce cas, SStot mesure la variation totale. SSreg mesure la variation expliquée et SSres mesure la variation inexpliquée.,
As SSres + SSreg = SStot, R2 = variation expliquée / Variation totale
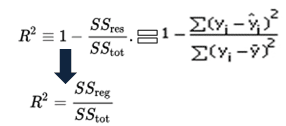
équation R-carré
R-carré est aussi appelé coefficient de détermination. Il se situe entre 0% et 100%. Une valeur r au carré de 100% signifie que le modèle explique toute la variation de la variable cible. Et une valeur de 0% mesure la puissance prédictive nulle du modèle. Valeur R au carré plus élevée, meilleur modèle.
ajusté R-carré
Il mesure la proportion de variation expliquée par seulement les variables indépendantes qui aident vraiment à expliquer la variable dépendante., Il vous pénalise pour ajouter une variable indépendante qui n’aide pas à prédire la variable dépendante.
Le R-carré ajusté peut être calculé mathématiquement en termes de somme des carrés. La seule différence entre l’équation R-carré et L’équation R-carré ajustée est le degré de liberté.
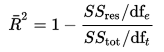
équation ajustée au carré r
Dans l’équation ci-dessus, dft est le degré de liberté n– 1 de l’estimation de la variance de population de la variable dépendante, et dfe est le degré de liberté n – p – 1 de l’estimation de la variance d’erreur de population sous-jacente.,
La valeur ajustée de R-carré peut être calculée en fonction de la valeur de r-carré, du nombre de variables indépendantes (prédicteurs), de la taille totale de l’échantillon.

équation R-carré ajustée 2
différence entre R-carré et R-carré ajusté
- chaque fois que vous ajoutez une variable indépendante à un modèle, le R-carré augmente, même si la variable indépendante est insignifiante. Il baisse jamais. Alors que le R-carré ajusté n’augmente que lorsque la variable indépendante est significative et affecte la variable dépendante.,
- r carré Ajusté peut être négatif lorsque r-squared est proche de zéro.
- La valeur R-carré ajustée doit toujours être inférieure ou égale à la valeur r-carré.
dans le tableau ci-dessous, le R-carré ajusté est maximal lorsque nous avons inclus deux variables. Il diminue lorsque la troisième variable est ajoutée. Alors que r-carré augmente lorsque nous avons inclus la troisième variable. Cela signifie que la troisième variable est insignifiante pour le modèle.

R-Squared vs adjusted R-Squared
le carré R ajusté doit être utilisé pour comparer des modèles avec différents nombres de variables indépendantes. Le carré R ajusté doit être utilisé lors de la sélection des prédicteurs importants (variables indépendantes) pour le modèle de régression.
R : calculez R-carré et R-carré ajusté
supposons que vous ayez des valeurs de variables dépendantes réelles et prédites. Dans le script ci-dessous, nous avons créé un exemple de ces valeurs. Dans cet exemple, y fait référence à la variable dépendante observée et yhat à la variable dépendante prédite.,
résultat Final: R-Squared = 0.6410828
supposons que vous ayez trois variables indépendantes dans ce cas.
n = 10
p = 3
adj.R.squared = 1 – (1 – R. squared) * ((n – 1)/(n-p-1))
print(adj.R.squared)
dans ce cas, la valeur 0.4616242 en supposant que nous avons 3 prédicteurs et 10 observations.