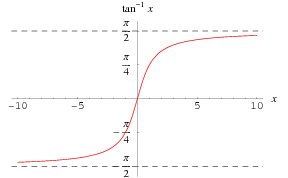
la inversa de La función tangente 
se traza sobre el eje real.
peor aún, la notación 
se utiliza a veces para el valor principal, con 
siendo utilizado para la función multivalor (Abramowitz y Stegun 1972, p. 80)., Tenga en cuenta que en la notación 
(comúnmente utilizado en América del Norte y en calculadoras de bolsillo en todo el mundo), 
denota la tangente y 
la función inversa, no la inversa multiplicativa.
el valor principal de la tangente inversa se implementa como ArcTan en Wolfram Language. En la biblioteca C de GNU, se implementa como atan (double x).,
la tangente inversa es una función multivalor y por lo tanto requiere un corte de rama en el plano complejo, que la Convención de Wolfram Language coloca en 
y 
., Esto se deduce de la definición de 
como
 |
(1)
|
En el Wolfram Language (y en este trabajo), esta rama de corte definición determina el rango de 
real 
. Sin embargo, se debe tener cuidado, ya que otras definiciones de corte de rama pueden dar diferentes rangos (más comúnmente, 
).,
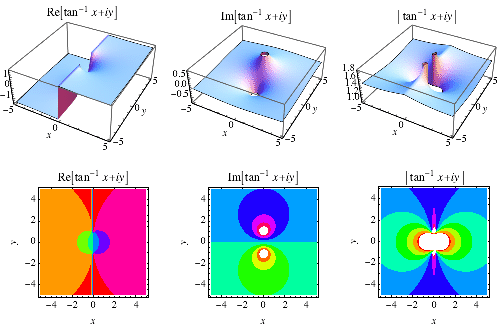
la inversa de La función tangente 
es colocado en el plano complejo.,
The complex argument of a complex number 
is often written as
 |
(9)
|
where 
, sometimes also denoted 
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of 
such that 
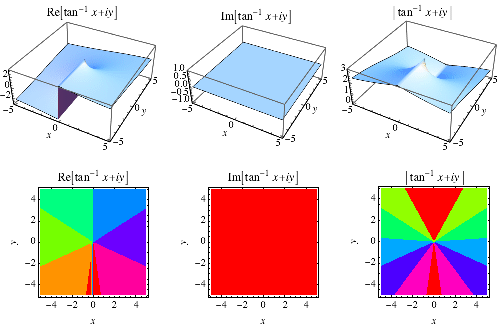
and 
. Plots of 
are illustrated above for real values of 
and 
.,
un tipo especial de tangente inversa que tiene en cuenta el cuadrante en el que 
se encuentra y es devuelto por el comando FORTRAN ATAN2(y, x), el comando de biblioteca C de GNU atan2(double y, double x), Y comando arctan, y a menudo está restringido al rango 
.,div> has the Maclaurin series of
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
 |
(13)
|
for real 
(Castellanos 1988).,interesting approximations to pi
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
(OEIS A075553 and A075554).,
In terms of the hypergeometric function,
 |
(28)
|
for complex 
, and
 |
(29)
|
for real 
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
 |
(36)
|
for 
, as well as the more complicated formula
 |
(37)
|
valid for all complex 
., An additional identity known to Euler is given by
 |
(38)
|
for 
or 
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
 |
(39)
|
where
 |
(40)
|
and 
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
para encontrar 
numéricamente, se puede usar el siguiente algoritmo aritmético-geométrico similar a la media.,464e247ac»>
and the inverse tangent is given by
 |
(47)
|
(Acton 1990).,
An inverse tangent 
with integral 
is called reducible if it is expressible as a finite sum of the form
 |
(48)
|
where 
are positive or negative integers and 
are integers 
., 
es reducible iff todos los factores primos de 
se producen entre los factores primos de 
para 
, …, 
. Una segunda condición necesaria y suficiente es que el mayor factor principal de 
es menor que 
., Equivalente a la segunda condición es la afirmación de que cada número de Gregory 
puede expresarse únicamente como una suma en términos de 
s para el cual 
es un número de Størmer (Conway y Guy 1996)., To find this decomposition, write
 |
(49)
|
so the ratio
 |
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
 |
(53)
|
where
 |
(54)
|
Todd (1949) gives a table of decompositions of 
for 
., Conway y Guy (1996) dan una tabla similar en términos de números de Størmer.,
the finding one of which is a given as a problem by Bailey et al., (2006, p. 225).