R-squared (R2)
mide la proporción de la variación en su variable dependiente explicada por todas sus variables independientes en el modelo. Asume que cada variable independiente en el modelo ayuda a explicar la variación en la variable dependiente., En realidad, algunas variables independientes (predictores) no ayudan a explicar la variable dependiente (objetivo). En otras palabras, algunas variables no contribuyen a predecir la variable objetivo.matemáticamente, R-cuadrado se calcula dividiendo la suma de cuadrados de residuos (SSres) por la suma total de cuadrados (SStot) y luego restarlo de 1. En este caso, sstot mide la variación total. Las medidas SSreg explicaron la variación y las medidas SSres la variación inexplicada.,
Como SSres + SSreg = SStot, R2 = variación explicada / variación Total
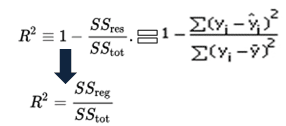
ecuación R-cuadrado
R-cuadrado también se llama coeficiente de determinación. Se encuentra entre el 0% y el 100%. Un valor R-cuadrado de 100% significa que el modelo explica toda la variación de la variable objetivo. Y un valor de 0% mide el poder predictivo cero del modelo. Mayor valor R-cuadrado, mejor el modelo.
R-cuadrado ajustado
mide la proporción de variación explicada solo por aquellas variables independientes que realmente ayudan a explicar la variable dependiente., Le penaliza por agregar variables independientes que no ayudan a predecir la variable dependiente.
Adjusted R-Squared can be calculated mathematically in terms of sum of squares. La única diferencia entre la ecuación R-cuadrado y R-cuadrado ajustado es el grado de libertad.
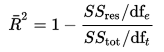
ecuación R-cuadrada ajustada
en la ecuación anterior, dft es los grados de libertad n– 1 de la estimación de la varianza poblacional de la variable dependiente, y dfe es los grados de libertad n – p – 1 de la estimación de la varianza de error poblacional subyacente.,
El valor ajustado de R-cuadrado se puede calcular basado en el valor de r-cuadrado, Número de variables independientes (predictores), tamaño total de la muestra.

ecuación R-cuadrada ajustada 2
diferencia entre R-cuadrado y R-cuadrado ajustado
- Cada vez que se agrega una variable independiente a un modelo, la R-cuadrada aumenta, incluso si la variable independiente es insignificante. Nunca declina. Mientras que R-cuadrado ajustado aumenta solo cuando la variable independiente es significativa y afecta a la variable dependiente.,
en la siguiente tabla, R-cuadrado ajustado es máximo cuando incluimos dos variables. Disminuye cuando se agrega la tercera variable. Mientras que R-cuadrado aumenta cuando incluimos tercera variable. Significa que la tercera variable es insignificante para el modelo.

R-Cuadrado vs Ajustado R-Cuadrado
Adjusted R-square should be used to compare models with different numbers of independent variables. Se debe usar R-cuadrado ajustado al seleccionar predictores importantes (variables independientes) para el modelo de regresión.
R: Calcule R-cuadrado y R-cuadrado ajustado
suponga que tiene valores de variables dependientes reales y predichos. En el siguiente script, hemos creado una muestra de estos valores. En este ejemplo, y se refiere a la variable dependiente observada y yhat se refiere a la variable dependiente predicha.,
resultado Final: R-Squared = 0.6410828
supongamos que tiene tres variables independientes en este caso.
n = 10
p = 3
adj.R.squared = 1 – (1 – R. squared) * ((n – 1)/(n-p-1))
print(adj.r.squared)
en este caso, el valor ajustado de R-squared es 0.4616242 asumiendo que tenemos 3 predictores y 10 observaciones.
Python: calcular R-cuadrado ajustado y R-cuadrado