|
crecimiento exponencial y decaimiento
MathBitsNotebook.com Topical Outline | Algebra 2 Outline | MathBits’ Teacher Resources Términos de Uso persona de contacto: Donna Roberts |
en Álgebra 1, se utilizaron las siguientes dos fórmulas de función para ilustrar fácilmente los conceptos de crecimiento y decadencia en situaciones aplicadas., Si una cantidad crece en un porcentaje fijo a intervalos regulares, el patrón puede ser representado por estas funciones.
|
Crecimiento Exponencial:
y = a(1 + r)x |
Decaimiento Exponencial:
y = a(1 – r)x |
Recuerde que el original exponencial de la fórmula es y = abx.notará que en estas nuevas funciones de crecimiento y decaimiento, el valor b (factor de crecimiento) ha sido reemplazado por (1 + r) o por (1 – r).,
La «tasa» de crecimiento (r) se determina como b = 1 + r.
La «tasa» de decaimiento (r) se determina como b = 1 – r
r = tasa de crecimiento o decaimiento (más a menudo representada como un porcentaje y expresada como un decimal)
x = número de intervalos de tiempo que han pasado
Ejemplo 1: la población de la ciudad natal es 2016 se estimó ser 35.000 personas con una tasa anual de incremento del 2,4%.a) ¿cuál es el factor de crecimiento de la ciudad natal?
Después de un año la población sería 35,000 + 0.024 (35000).,
por factorización, tenemos 35000(1 + 0.024) o 35000 (1.024).el factor de crecimiento es 1.024. (Recuerde que el factor de crecimiento es mayor que 1.)
|
b) escriba una ecuación para modelar el crecimiento futuro.
y = abx = a (1.014)x = 35000 (1.024) x c) utilice la ecuación para estimar la población en 2020 a las cien personas más cercanas. |
 |
la Mayoría de los fenómenos que ocurren naturalmente a crecer de forma continua. Por ejemplo, las bacterias continuarán creciendo durante un período de 24 horas, produciendo nuevas bacterias que también crecerán. Las bacterias no esperan hasta el final de las 24 horas, y luego todas se reproducen a la vez.
La E exponencial se usa cuando se modela el crecimiento continuo que ocurre naturalmente, como poblaciones, bacterias,desintegración radiactiva, etc., Puedes pensar en e como una constante universal que representa lo rápido que podrías crecer usando un proceso continuo. Y, la belleza de e es que no solo se utiliza para representar el crecimiento continuo, sino que también puede representar el crecimiento medido periódicamente a través del tiempo (como el crecimiento en el Ejemplo 1).
en Álgebra 2, La exponencial e se utilizará en situaciones de crecimiento continuo o decaimiento. La siguiente fórmula se utiliza para ilustrar el crecimiento continuo y la decadencia. Si una cantidad crece continuamente en un porcentaje fijo, el patrón puede ser representado por esta función.,
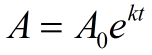
A0 = valor inicial (cantidad antes de medir el crecimiento o decaimiento)
E = exponencial e = 2.71828183…,
k = tasa de crecimiento continuo (también llamada constante de proporcionalidad)
(k > 0, la cantidad está aumentando (creciendo); k < 0, la cantidad está disminuyendo (decayendo))
t = tiempo que ha pasado
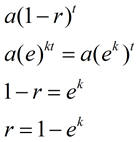 |
si comparamos esta nueva fórmula con nuestra anterior fórmula de decaimiento exponencial (o fórmula de crecimiento), podemos ver cómo ek se relaciona con la tasa de decaimiento, r, (o crecimiento)., |
(bacterias crecen continuamente)
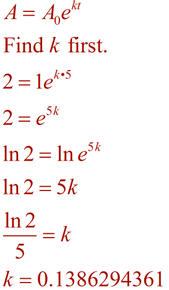 |
Ahora, la forma de la ecuación usando este valor de k, y resolver el problema utilizando el tiempo de 96 minutos.,
|
![]()