R-squared (R2)
It-foranstaltninger, at den andel af variation i de afhængige variable forklares ved, at alle dine uafhængige variabler i modellen. Det antages, at hver uafhængig variabel i modellen hjælper med at forklare variation i den afhængige variabel., I virkeligheden hjælper nogle uafhængige variabler (forudsigere) ikke med at forklare afhængig (mål) variabel. Med andre ord bidrager nogle variabler ikke til at forudsige målvariablen.
matematisk beregnes R-kvadreret ved at dividere summen af kvadrater af rester (SSR ‘ er) med den samlede sum af kvadrater (SStot) og derefter trække den fra 1. I dette tilfælde måler SStot den samlede variation. SSreg måler forklaret variation og SSR måler uforklarlig variation.,
Som SSres + SSreg = SStot, R2 = Forklarede variation / Samlede Variation
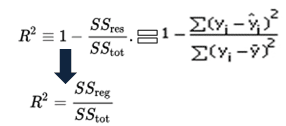
f R-squared Ligning
R-Squared er også kaldet determinationskoefficienten. Den ligger mellem 0% og 100%. En R-kvadreret værdi på 100% betyder, at modellen forklarer al variationen af målvariablen. Og en værdi på 0% måler nul prædiktiv effekt af modellen. Højere R-kvadreret værdi, bedre modellen.
justeret R-kvadreret
Det måler andelen af variation forklaret med kun de uafhængige variabler, der virkelig hjælper med at forklare den afhængige variabel., Det straffer dig for at tilføje uafhængig variabel, der ikke hjælper med at forudsige den afhængige variabel.
justeret R-kvadreret kan beregnes matematisk i form af summen af kvadrater. Den eneste forskel mellem R-S .uare og justeret r-s .uare ligning er graden af frihed.
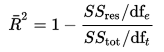
Justeret R-Kvadreret Ligning
I ovenstående ligning, dft er antallet af frihedsgrader n– 1 af estimatet af befolkningen variansen i den afhængige variabel, og dfe er antallet af frihedsgrader n – p – 1 af estimatet af den underliggende befolkning fejl varians.,
justeret R-kvadreret værdi kan beregnes ud fra værdien af r-kvadreret, antal uafhængige variabler (forudsigere), samlet prøvestørrelse.

Justeret R-Kvadreret Ligning 2
Forskellen mellem R-pladsen og Justeret R-square
- Hver gang du tilføjer en uafhængig variabel til en model, R-squared stiger, selv hvis den uafhængige variable er insignifikante. Det falder aldrig. Mens justeret r-s .uared kun stiger, når uafhængig variabel er signifikant og påvirker afhængig variabel.,
- Justeret r-kvadreret kan være negativ, når den r-kvadrerede er tæt på nul.
- justeret r-s .uared værdi altid være mindre end eller lig med r-S .uared værdi.
i tabellen nedenfor er justeret r-kvadreret maksimalt, når vi inkluderede to variabler. Det falder, når tredje variabel tilføjes. Mens r-kvadreret stiger, når vi inkluderede tredje variabel. Det betyder, at tredje variabel er ubetydelig for modellen.

f R-Squared vs. Justeret R-Kvadreret
justeret R-S .uare bør bruges til at sammenligne modeller med forskellige antal uafhængige variabler. Justeret R-S .uare skal bruges, mens du vælger vigtige forudsigere (uafhængige variabler) for regressionsmodellen.
R : Beregn R-S .uared og justeret R-S .uared
Antag, at du har faktiske og forudsagte afhængige variable værdier. I scriptet nedenfor har vi oprettet en prøve af disse værdier. I dette eksempel henviser y til den observerede afhængige variabel, og yhat henviser til den forudsagte afhængige variabel.,
slutresultat : R-S .uared = 0.6410828
Lad os antage, at du har tre uafhængige variabler i dette tilfælde.
n = 10
s = 3
adj.r.squared = 1 – (1 – R. squared) * ((n – 1)/(n-p-1))
print(adj.r.squared)
I dette tilfælde, justeret r-kvadreret værdi er 0.4616242 forudsat at vi har 3 prædiktorer og 10 observationer.