|
Eksponentiel Vækst og Forfald
MathBitsNotebook.com Aktuelle Disposition | Algebra 2 Skitse | MathBits’ lærerressourcer Betingelser for Brug Kontaktperson: Donna Roberts |
I Algebra 1, de to følgende funktion formler, der anvendes til nemt at illustrere begreberne vækst og forfald i anvendt situationer., Hvis en mængde vokser med en fast procent med jævne mellemrum, kan mønsteret afbildes af disse funktioner.
|
Eksponentiel Vækst:
y = a(1 + r)x |
Eksponentielle Henfald:
y = a(1 – r)x |
Husk, at den oprindelige eksponentiel formlen y = abx.
du vil bemærke, at i disse nye vækst – og forfaldsfunktioner er
b-værdien (vækstfaktor) blevet erstattet enten med (1 + r) eller med (1-r).,
vækst “sats” (f) bestemmes som b = 1 + r.
forfald “sats” (f) bestemmes som b = 1 – r
r = vækst eller forfald sats (oftest repræsenteret som en procentdel og udtrykt som en decimal)
x = antallet af tidsintervaller, der er gået
Eksempel 1: Befolkningen i Hjemby er 2016 blev anslået til 35.000 mennesker med en årlig stigning på 2,4%.
a) Hvad er vækstfaktoren for hjemby?
efter et år ville befolkningen være 35,000 + 0.024(35000).,
ved factoring har vi 35000(1 + 0.024) eller 35000 (1.024).
vækstfaktoren er 1.024. (Husk, at vækstfaktor er større end 1.)
|
b) Skriv en ligning til model fremtidig vækst.
y = AB. = a(1.014). = 35000(1.024). c) brug ligningen til at estimere befolkningen i 2020 til de nærmeste hundrede mennesker. |
 |
![]()
de Fleste naturligt forekommende fænomener vokse kontinuerligt. For eksempel vil bakterier fortsætte med at vokse over en 24 timers periode, der producerer nye bakterier, som også vil vokse. Bakterierne venter ikke til slutningen af de 24 timer, og så reproducerer alle på .n gang.
den eksponentielle e bruges til modellering af kontinuerlig vækst, der forekommer naturligt, såsom populationer, bakterier, radioaktivt henfald osv., Du kan tænke på e som en universel konstant, der repræsenterer, hvor hurtigt du muligvis kunne vokse ved hjælp af en kontinuerlig proces. Og skønheden ved e er, at det ikke kun bruges til at repræsentere kontinuerlig vækst, men det kan også repræsentere vækst målt periodisk over tid (såsom væksten i Eksempel 1).
i Algebra 2 vil den eksponentielle e blive brugt i situationer med kontinuerlig vækst eller forfald. Følgende formel bruges til at illustrere kontinuerlig vækst og forfald. Hvis en mængde vokser kontinuerligt med en fast procent, kan mønsteret afbildes ved denne funktion.,
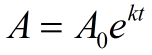
A0 = startværdi (beløb før måling af vækst eller forfald)
e = eksponentiel e = 2.71828183…,
k = konstant vækstrate (også kaldet konstant om proportionalitet)
k > 0, mængden er stigende (voksende); k < 0, beløbet er faldende (rådnende))
t = tid, der er gået
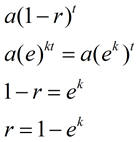 |
Hvis vi sammenligner denne nye formel til vores tidligere eksponentielle henfald formel (eller vækst formel), vi kan se, hvor ek er relateret til henfaldet, r, (eller vækst)., |
(bakterier løbende at vokse)
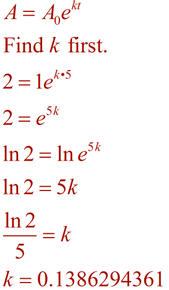 |
Nu, form ligningen ved hjælp af denne k-værdi, og løse problemet ved hjælp af den tid, 96 minutter.,
|
![]()