![]()
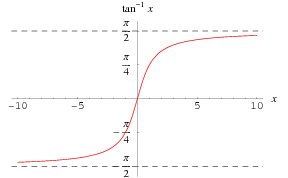
inverzní funkce tangens ![]() je vynesena výše podél reálné osy.
je vynesena výše podél reálné osy.
ještě Horší je, že zápis ![]() je někdy používán pro hlavní hodnotou, s
je někdy používán pro hlavní hodnotou, s ![]() se používá pro vícehodnotové funkce (Abramowitzová a Stegun 1972, str. 80)., Všimněte si, že v notaci
se používá pro vícehodnotové funkce (Abramowitzová a Stegun 1972, str. 80)., Všimněte si, že v notaci ![]() (běžně používané v Severní Americe a v kapesní kalkulačky po celém světě),
(běžně používané v Severní Americe a v kapesní kalkulačky po celém světě), ![]() označuje tečnou a
označuje tečnou a ![]() inverzní funkce, není multiplikativní inverzní.
inverzní funkce, není multiplikativní inverzní.
hlavní hodnota inverzní tangenty je implementována jako ArcTan v jazyce Wolfram. V knihovně GNU C je implementován jako atan (double x).,

inverzní tangens je vícehodnotové funkce, a proto vyžaduje větev řez v komplexní rovině, které Wolfram Jazyk je konvence místa na ![]()
![]() ., To vyplývá z definice
., To vyplývá z definice ![]() jako
jako
|
(1)
|
Ve Wolfram Jazyk (a v této práci), tato větev řez definice určuje rozsah ![]() skutečné
skutečné ![]()
![]() . Péče musí být přijata, nicméně, jako další větve cut definice může dát různé rozsahy (nejčastěji,
. Péče musí být přijata, nicméně, jako další větve cut definice může dát různé rozsahy (nejčastěji, ![]() ).,
).,
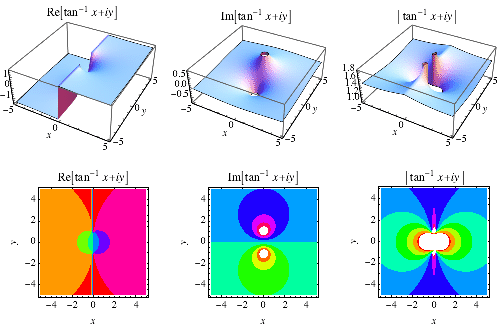
inverzní funkce tangens ![]() je vynesena výše v komplexní rovině.,
je vynesena výše v komplexní rovině.,


The complex argument of a complex number ![]() is often written as
is often written as
|
(9)
|
where ![]() , sometimes also denoted
, sometimes also denoted ![]() , corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of
, corresponds to the counterclockwise angle from the positive real axis, i.,e., the value of ![]() such that
such that ![]() and
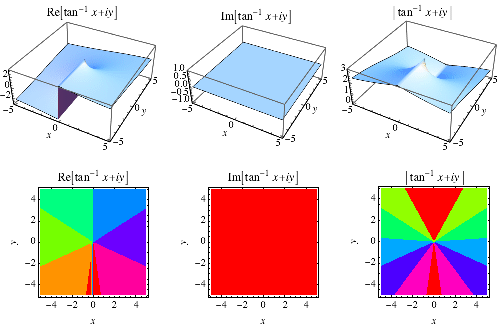
and ![]() . Plots of
. Plots of ![]() are illustrated above for real values of
are illustrated above for real values of ![]() and
and ![]() .,
.,
zvláštní druh inverzní tangens, který bere v úvahu kvadrantu, ve kterém ![]() leží a je vrácena FORTRAN příkaz ATAN2(y, x), GNU C knihovna příkaz atan2(double y, double x), a Wolfram Language příkaz ArcTan, a je často omezeno na rozsah
leží a je vrácena FORTRAN příkaz ATAN2(y, x), GNU C knihovna příkaz atan2(double y, double x), a Wolfram Language příkaz ArcTan, a je často omezeno na rozsah ![]() .,div> has the Maclaurin series of
.,div> has the Maclaurin series of
|
(11)
|
|||
|
(12)
|
(OEIS A033999 and A005408).,A more rapidly converging form due to Euler is given by
|
(13)
|
for real ![]() (Castellanos 1988).,interesting approximations to pi
(Castellanos 1988).,interesting approximations to pi
|
(16)
|
|||
|
(17)
|
(OEIS A075553 and A075554).,

In terms of the hypergeometric function,
|
(28)
|
for complex ![]() , and
, and
|
(29)
|
for real ![]() (Castellanos 1988).,
(Castellanos 1988).,
The inverse tangent satisfies the addition formula
|
(36)
|
for ![]() , as well as the more complicated formula
, as well as the more complicated formula
|
(37)
|
valid for all complex ![]() ., An additional identity known to Euler is given by
., An additional identity known to Euler is given by
|
(38)
|
for ![]() or
or ![]() ., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
., Another interesting inverse tangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1991, Castellanos 1988) is
|
(39)
|
where
|
(40)
|
and ![]() .,
.,
The inverse tangent has continued fractionrepresentations
 |
(41)
|
(Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138) and
 |
(42)
|
due to Euler and sometimes known as Euler’scontinued fraction (Borwein et al. 2004, p. 30).,
Chcete-li najít ![]() číselně lze použít následující aritmeticko-geometrický střední algoritmus.,464e247ac“>
číselně lze použít následující aritmeticko-geometrický střední algoritmus.,464e247ac“>
and the inverse tangent is given by
|
(47)
|
(Acton 1990).,
An inverse tangent ![]() with integral
with integral ![]() is called reducible if it is expressible as a finite sum of the form
is called reducible if it is expressible as a finite sum of the form
|
(48)
|
where ![]() are positive or negative integers and
are positive or negative integers and ![]() are integers
are integers ![]() .,
., ![]() je redukovatelné iff všechny primární faktory
je redukovatelné iff všechny primární faktory ![]() vyskytují mezi hlavní faktory
vyskytují mezi hlavní faktory ![]()
![]() …,
…, ![]() . Druhou nutnou a postačující podmínkou je, že největší prvočíslo
. Druhou nutnou a postačující podmínkou je, že největší prvočíslo ![]() je menší než
je menší než ![]() ., Ekvivalentní druhou podmínkou je prohlášení, že každý Gregory číslo
., Ekvivalentní druhou podmínkou je prohlášení, že každý Gregory číslo ![]() může být jednoznačně vyjádřeno jako součet, pokud jde o
může být jednoznačně vyjádřeno jako součet, pokud jde o ![]() y, pro které
y, pro které ![]() je Størmer číslo (Conway a Chlap, 1996)., To find this decomposition, write
je Størmer číslo (Conway a Chlap, 1996)., To find this decomposition, write
|
(49)
|
so the ratio
|
(50)
|
is a rational number.,ba555fd751″>
allows a direct conversion to a corresponding inversecotangent formula
|
(53)
|
where
|
(54)
|
Todd (1949) gives a table of decompositions of ![]() for
for ![]() ., Conway a Guy (1996) dávají podobnou tabulku, pokud jde o čísla Størmer.,
., Conway a Guy (1996) dávají podobnou tabulku, pokud jde o čísla Størmer.,


the finding one of which is a given as a problem by Bailey et al., (2006, s. 225).