|
exponenciální růst a úpadek
MathBitsNotebook.com aktuální obrys | Algebra 2 obrys | Mathbits‘ učitel zdroje Podmínky použití Kontaktní osoba: Donna Roberts |
v algebře 1 byly použity následující dvě funkční vzorce pro snadné ilustraci konceptů růstu a rozpadu v aplikovaných situacích., Pokud množství roste v pravidelných intervalech o pevné procento, může být vzor zobrazen těmito funkcemi.
|
exponenciální růst:
y = a(1 + r)x |
exponenciální rozpad:
y = a(1 – r)x |
nezapomeňte, že původní exponenciální vzorec byl y = ABX.
všimnete si, že v těchto nových růstových a rozpadových funkcích byla hodnota b (růstový faktor) nahrazena buď (1 + r) nebo (1 – r).,
růstová „rychlost“ (r) se stanoví jako b = 1 + r.
rychlost rozpadu „(r) se stanoví jako B = 1 – r
R = rychlost růstu nebo rozpadu (nejčastěji reprezentovaná jako procento a vyjádřená jako desetinná hodnota)
x = počet časových intervalů, které prošly
Příklad 1: populace rodného města je 2016 byla odhadnuta na být 35.000 lidí s ročním tempem zvýšení o 2,4%.
a) jaký je růstový faktor pro rodné město?
po jednom roce by populace byla 35,000 + 0.024 (35000).,
factoringem máme 35000(1 + 0.024) nebo 35000 (1.024).
růstový faktor je 1,024. (Pamatujte, že růstový faktor je větší než 1.)
|
b) napište rovnici pro modelování budoucího růstu.
y = abx = a(1.014)x = 35000(1.024)x c) použijte rovnici k odhadu populace v roce 2020 na nejbližší stovku lidí. |
![]()
většina přirozeně se vyskytujících jevů neustále roste. Například bakterie budou i nadále růst po dobu 24 hodin a budou produkovat nové bakterie, které také porostou. Bakterie nečekají až do konce 24 hodin a pak se všechny reprodukují najednou.
exponenciální e se používá při modelování kontinuálního růstu, který se přirozeně vyskytuje, jako jsou populace,bakterie, radioaktivní rozpad atd., Můžete myslet na e jako na univerzální konstantu představující, jak rychle byste mohli růst pomocí nepřetržitého procesu. A krásu e je, že nejen, že je používán reprezentovat kontinuální růst, ale to může také reprezentovat růst měří pravidelně v čase (např. růst v Příkladu 1).
v algebře 2 se exponenciální e použije v situacích nepřetržitého růstu nebo rozpadu. Následující vzorec se používá k ilustraci nepřetržitého růstu a rozpadu. Pokud množství roste nepřetržitě o pevné procento, může být tento vzor zobrazen touto funkcí.,
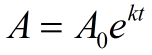
A0 = počáteční hodnota (částka před měřením růst, nebo úpadek)
e = exponenciální e = 2.71828183…,
k = trvalé tempo růstu (také se nazývá konstanta proporcionality)
(k > 0, částka je zvyšující se (rostoucí); k < 0, částka je klesající (rozpadající se))
t = čas, který uplynul
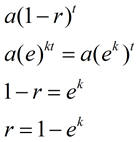 |
Pokud budeme srovnávat tento nový vzorec na naše předchozí vzorce na výpočet rozpadu (nebo růstové vzorce), můžeme vidět, jak ek souvisí s rychlostí rozkladu, r, (nebo růst)., |
(bakterie neustále rostou)
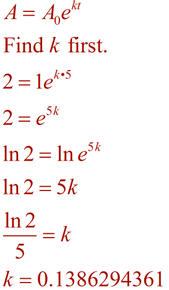 |
Nyní, tvořit rovnice pomocí tohoto hodnota k, a vyřešit problém pomocí časové 96 minut.,
|
![]()